1. If the graduate applies to all 10 companies, what is the probability that she will get...
Question:
1. If the graduate applies to all 10 companies, what is the probability that she will get at least one offer?
2. If she can apply to only one company, based on cost and success probability criteria alone, should she apply to company 5? Why or why not?
3. If she applies to companies 2, 5, 8, and 9, what is the total cost? What is the probability that she will get at least one offer?
4. If she wants to be at least 75% confident of getting at least one offer, to which companies should she apply to minimize the total cost? (This is a trial-and-error problem.)
5. If she is willing to spend $1,500, to which companies should she apply to maximize her chances of getting at least one job?
A business graduate wants to get a job in any one of the top 10 accounting firms. Applying to any of these companies requires a lot of effort and paperwork and is therefore costly. She estimates the cost of applying to each of the 10 companies and the probability of getting a job offer there. These data are tabulated below. The tabulation is in the decreasing order of cost.
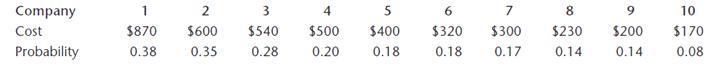
Step by Step Answer:

Complete Business Statistics
ISBN: 9780077239695
7th Edition
Authors: Amir Aczel, Jayavel Sounderpandian





