A rectangular array of mn numbers arranged in n rows, each consisting of m columns, is said to contain a saddlepoint if there is a number that is both the minimum of its row and the maximum of its column. For instance, in the array

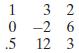
the number 1 in the first row, first column is a saddlepoint. The existence of a saddlepoint is of significance in the theory of games. Consider a rectangular array of numbers as described previously and suppose that there are two individuals— A and B—that are playing the following game: A is to choose one of the numbers 1, 2, . . . , n and B one of the numbers 1, 2, . . . ,m. These choices are announced simultaneously, and if A chose i and B chose j, then A wins from B the amount specified by the number in the ith row, jth column of the array. Now suppose that the array contains a saddlepoint—say the number in the row r and column k—call this number x_rk. Now if player A chooses row r, then that player can guarantee herself a win of at least x_rk (since x_rk is the minimum number in the row r). On the other hand, if player B chooses column k, then he can guarantee that he will lose no more than x_rk (since x_rk is the maximum number in the column k). Hence, as A has a way of playing that guarantees her a win of x_rk and as B has a way of playing that guarantees he will lose no more than x_rk, it seems reasonable to take these two strategies as being optimal and declare that the value of the game to player A is x_rk.

If the nm numbers in the rectangular array described are independently chosen from an arbitrary continuous distribution, what is the probability that the resulting array will contain a saddle-point?

Transcribed Image Text:

2 105 9