A statistician has to decide on the basis of a single observation whether the parameter of

A statistician has to decide on the basis of a single observation whether the parameter θ of the density

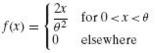
Equals θ₁ or θ₂, where θ₁ < θ₂. If he decides on θ₁ when the observed value is less than the constant k, on θ₂ when the observed value is greater than or equal to the constant k, and he is fined C dollars for making the wrong decision, which value of k will minimize the maximum risk?

Transcribed Image Text:

2T for 0 < x < θ elsewhere f(x)= 0