An airline plans to initiate service at an airport in a city of approximately 500,000 people. To determine staffing requirements, officials for the airline take advantage of the sample survey data on the relationship between the number of flights per week and the number of employees for 30 airlines at various airports in cities that are similar in size (approximately 300,000 to 700,000). The data is found below.

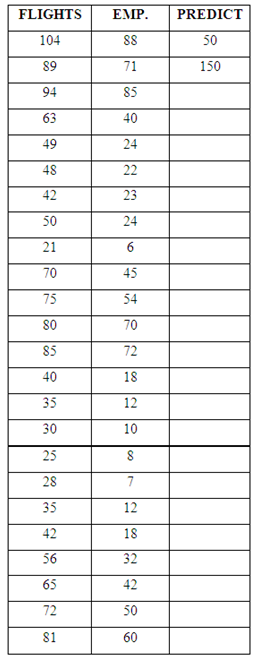
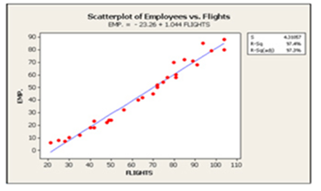
Regression Analysis: EMP. versus FLIGHTS

The regression equation is

EMP. = - 23.3 + 1.04 FLIGHTS

Predictor      Coef  SE Coef       T      P

Constant    -23.261    2.177  -10.68  0.000

FLIGHTS     1.04407  0.03202   32.60  0.000

S = 4.31057   R-Sq = 97.4%   R-Sq(adj) = 97.3%

Analysis of Variance

Source          DF      SS      MS        F      P

Regression       1   19752   19752  1063.00  0.000

Residual Error 28     520      19

Total           29   20272

Predicted Values for New Observations

New Obs      Fit  SE Fit       95% CI            95% PI

      1   28.943   0.896  ( 27.107,  30.779)  ( 19.924,  37.961)

      2  133.350   2.883  (127.445, 139.255)  (122.728, 143.973)XX

XX denotes a point that is an extreme outlier in the predictors.

Values of Predictors for New Observations

New .........Obs FLIGHTS      

1.........................50      

2.......................150

Correlations: FLIGHTS, EMP.

Pearson correlation of FLIGHTS and EMP. = 0.987

P-Value = 0.000

a. Analyze the above output to determine the regression equation.

b. Find and interpret βˆ1 in the context of this problem.

c. Find and interpret the coefficient of determination (r-squared).

d. Find and interpret coefficient of correlation.

e. Does the data provide significant evidence (α = .05) that the number of flights can be used to predict the number of employees? Test the utility of this model using a two-tailed test. Find the observed p-value and interpret.

f. Find the 95% prediction interval for the number of employees needed for an airline that has 50 flights per week. Interpret this interval.

g. Find the 95% confidence interval for the mean number of employees needed for airlines that have 50 flights per week. Interpret this interval.

h. What can we say about the number of employees needed for an airport that has 150 flights per week?

Transcribed Image Text:

PREDICT FLIGHTS EMP. 104 88 50 89 71 150 94 85 63 40 49 24 48 22 42 23 50 24 21 70 45 75 54 80 70 85 72 40 18 35 12 30 10 25 28 35 12 42 18 56 32 65 42 72 50 81 60