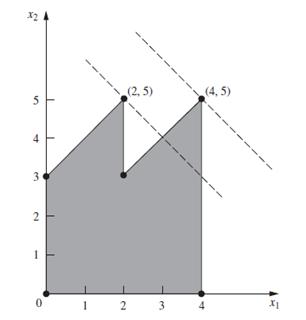
Consider a two-variable mathematical programming problem that has the feasible region shown on the graph, where the
Question:
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction to Operations Research
ISBN: 978-1259162985
10th edition
Authors: Frederick S. Hillier, Gerald J. Lieberman
Question Posted:





