Consider the sampling distribution of given in Table 7.5. a. Calculate the value of using the formula = P(). Is the value of

Consider the sampling distribution of given in Table 7.5.
a. Calculate the value µ of using the formula µ = ˆ‘P(). Is the value of µ calculated in Exercise 7.6 the same as the value of µ calculated here?
b. Calculate the value of σ by using the formula

c. From Exercise 7.6, σ = 8.09. Also, our sample size is 3, so that n = 3. Therefore σ/ˆšn = 8.09/ˆš3 = 4.67. From part b, you should get σ = 3.30. Why does σ/ˆšn not equal σ in this case?
d. In our example (given in the beginning of Section 7.1) on scores, N = 5 and n = 3. Hence, n/N = 3/5 = .60. Because n/N is greater than .05, the appropriate formula to find σ is

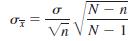
Show that the value of calculated by using this formula gives the same value as the one calculated in part b above.

oz = Vr'P(x) ()