For each of the following, determine c so that the function can serve as the probability distribution
Question:
For each of the following, determine c so that the function can serve as the probability distribution of a random variable with the given range:
(a) f(x) = cx for x = 1, 2, 3, 4, 5;
(b)
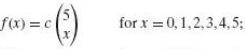
(c) f(x) = cx2 for x = 1, 2, 3, . . . , k;
(d)
The word "distribution" has several meanings in the financial world, most of them pertaining to the payment of assets from a fund, account, or individual security to an investor or beneficiary. Retirement account distributions are among the most...
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
a c1 2 3 5 1 thus C 115 b c5 52 53 54 1 1 thus c 12137 c From The...View the full answer
Answered By
Somshukla Chakraborty
I have a teaching experience of more than 4 years by now in diverse subjects like History,Geography,Political Science,Sociology,Business Enterprise,Economics,Environmental Management etc.I teach students from classes 9-12 and undergraduate students.I boards I handle are IB,IGCSE, state boards,ICSE, CBSE.I am passionate about teaching.Full satisfaction of the students is my main goal.
I have completed my graduation and master's in history from Jadavpur University Kolkata,India in 2012 and I have completed my B.Ed from the same University in 2013. I have taught in a reputed school of Kolkata (subjects-History,Geography,Civics,Political Science) from 2014-2016.I worked as a guest lecturer of history in a college of Kolkata for 2 years teaching students of 1st ,2nd and 3rd year. I taught Ancient and Modern Indian history there.I have taught in another school in Mohali,Punjab teaching students from classes 9-12.Presently I am working as an online tutor with concept tutors,Bangalore,India(Carve Niche Pvt.Ltd.) for the last 1year and also have been appointed as an online history tutor by Course Hero(California,U.S) and Vidyalai.com(Chennai,India).
2+ Reviews
10+ Question Solved
Related Book For 
John E Freunds Mathematical Statistics With Applications
ISBN: 9780134995373
8th Edition
Authors: Irwin Miller, Marylees Miller
Question Posted:
