For small sample cases where we are testing the difference between two population means, when the population standard deviations are unknown, we used an approach in which we assumed that the two population standard deviations were equal. Under this assumption, we pooled the sample standard deviations and ultimately used the t distribution with n₁ + n₂ – 2 degrees of freedom to conduct the test. If we assume that the population standard deviations are unequal, we would need to modify our approach. One alternative is to use what’s known as the WelchSatterwaite method. In this procedure, we won’t pool the sample standard deviations and we’ll use the t distribution with degrees of freedom computed as

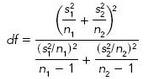
The result of this df calculation can be rounded down to the next lower integer value. We’ll estimate the standard error of the sampling distribution as

Situation: Two groups of 15 consumers each were asked to read through a magazine that contains your company’s ad in one of two versions. One sample group was given the magazine containing version A of the ad; the other, version B. Each group was then asked to list as many ad and product details as they could recall. For the version A group, the average number of details was 10.2, with a standard deviation of 5.4. For the version B group, the average was 7.2, with a standard deviation of 3.9. 

a. Using a significance level of .05, construct the appropriate hypothesis test to test a null hypothesis that there’s no difference in the average recall rate for the two ad versions. Assume that the two population distributions represented have unequal standard deviations. 

b. Compare your result in part a to the result you would produce if you assume that the two population distributions have equal standard deviations.

n, n. af = n,-1 n2 1