Given large random samples from two binomial populations, show that the null hypothesis 1 =
Question:
Given large random samples from two binomial populations, show that the null hypothesis θ1 = θ2 can be tested on the basis of the statistic
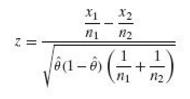
Where
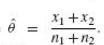
Transcribed Image Text:
1122 n2 X1+12 1 +n2 θ=
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 80% (10 reviews)
Has approximately standard normal d...View the full answer

Answered By

Muhammad Umair
I have done job as Embedded System Engineer for just four months but after it i have decided to open my own lab and to work on projects that i can launch my own product in market. I work on different softwares like Proteus, Mikroc to program Embedded Systems. My basic work is on Embedded Systems. I have skills in Autocad, Proteus, C++, C programming and i love to share these skills to other to enhance my knowledge too.
3.50+
1+ Reviews
10+ Question Solved
Related Book For 

John E Freunds Mathematical Statistics With Applications
ISBN: 9780134995373
8th Edition
Authors: Irwin Miller, Marylees Miller
Question Posted:
Students also viewed these Statistics questions
-
Random samples from two binomial populations yielded the following statistics: p1 = .45 n1 = 100 p2 = .40 n2 = 100 a. Calculate the p-value of a test to determine whether we can infer that the...
-
Independent random samples, each containing 800 observations, were selected from two binomial populations. The samples from populations 1 and 2 produced 320 and 400 successes, respectively. a. Test...
-
Independent random samples were selected from two binomial populations. The size and number of observed successes for each sample are shown in the following table: Sample 1Sample 2 n1 = 200 .....n2 =...
-
Seanna OBrien receives pension payments of $3200 at the end of every six months from a retirement fund of $50 000. The fund earns 7% compounded semi-annually. (a) How many payments will Seanna...
-
A recent survey of New York State families asked about their vacation habits. The accompanying two-way table shows the number of families according to where they live (rural, suburban, urban) and the...
-
Under what conditions is goodwill recorded?
-
Explain the difference between the Address and Addresses classes.
-
I don't see that in my intermediate accounting text I saved from college, you explain to another member of the accounting division of Dowell Chemical Corporation. This will take some research. Your...
-
Saturna Corporation began Year 6 with the following account balances: Common shares, 1 0 0 , 0 0 0 shares authorized, 5 0 , 0 0 0 issued $ 1 , 2 0 0 , 0 0 0 Retained earnings 9 5 0 , 0 0 0 During...
-
FlyHigh Tech, an early-stage startup, reports to its investors using a balanced scorecard that is prepared at the end of each quarter. During the first and second quarters of the current year, the...
-
For k = 2, show that the 2 formula on page 369 can be written as (2)(n2-n12)
-
Show that the square of the expression for z in Exercise 13.12 equals So that the two tests are actually equivalent when the alternative hypothesis is θ1 θ2. The test...
-
Many producers are now seeking new opportunities in international markets. Are the opportunities for international expansion equally good for retailers? Explain your answer.
-
Bushmills Irish Whiskey, a world-renowned brand of Diageo plc, is distilled in County Antrim in Northern Ireland. The Old Bushmills distillery has been in operation since 1608 and currently markets...
-
Government crime-fighting targets are a shambles and should be scrapped, claims Chief Superintendent, Ian Johnston. Mr Johnston was speaking ahead of the Police Superintendents Associations annual...
-
Asda is staging a major push south opening 11 new stores in the greater London region over the next few months with plans for a further 150 by 2018.Two of the new stores will be a trial of a new...
-
The British government has pledged to spend 0.7 per cent of national aid resulting in 12 billion being allocated to the Department for International Developments (DfIDs) aid budget despite the fact...
-
The term TetraPak is one which is familiar to most consumers it is the name you will see on the card cartons in which milk, juice and other liquid products are frequently packaged. The Tetra group...
-
Use the tables to evaluate the following. x012 3 5 f(x) 1 1 2 0 2 1 x-1 3 4 3 4 4 2 4 5
-
Consider the sections of two circuits illustrated above. Select True or False for all statements.After connecting a and b to a battery, the voltage across R1 always equals the voltage across R2.Rcd...
-
The price of Albertson stock increased on 40% of the trading days over the past year. The price of Boeing stock increased on 30% of the trading days. On 60% of the days that the price of Albertson...
-
A scientific study indicates that if there is an explosive volcanic eruption (Event A) in the tropics, the probability of an El Nino event (Event B) during the following winter increases...
-
Antonia and Byron are both due at the office of Ethan-Davies, Inc. for an important business meeting and both are running late. Antonia calls in and says that its only 40% likely that she will get to...
-
Enmebaragesi of Kish, Inc. has sales of $282,000, cost of goods sold of $206,000, depreciation of $4,200, and interest expense of $22,000. The tax rate is 30.8 percent. What is the times interest...
-
Inkishush and Company has a book value per share of $10.35, earnings per share of $2.23, and a price-earnings ratio of 19.4. What is the market-to-book ratio?
-
The Chaldean Riverfood Market has sales of $38,200, current assets of $8,100, net income of $2,600, fixed assets of $12,500, total debt of $10,600, and dividends of $915. What is the sustainable...

Study smarter with the SolutionInn App


