If X 1 and X 2 are the means of independent random samples of sizes n 1 and n 2 from a normal population with the mean and the variance 2 , show that the variance of the unbiased estimator Is a minimum when n 1 n 1 n 2 X (1 w) X2...

If X 1 and X 2 are the means of independent random samples of sizes n 1

Question:

If X̅₁ and X̅₂ are the means of independent random samples of sizes n₁ and n₂ from a normal population with the mean µ and the variance σ², show that the variance of the unbiased estimator

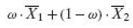
Is a minimum when ω = n₁ / n₁ + n₂

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

John E Freunds Mathematical Statistics With Applications

ISBN: 9780134995373

8th Edition

Authors: Irwin Miller, Marylees Miller

See More Books

Question Posted: Nov 04, 2015 03:32 AM

See More Questions

One property of the mean is that if we know the means and sample sizes of two (or more) data sets, we can calculate the combined mean of both (or all) data sets. The combined mean for two data sets...
The data for a random sample of six paired observations are shown in the next table. a. Calculate the difference between each pair of observations by subtracting observation 2 from observation 1. Use...
Two independent random samples of sizes n1 = 4 and n2 = 5 are selected from each of two normal populations: a. Calculate s2, the pooled estimator of s2. b. Find a 90% confidence interval for (1 - 2),...
2) WWW.myitlab.com is an example of a(n). O domain name O protocol prefix OURL omni box
The employees at a General Motors assembly plant are polled as they leave work. Each is asked, What brand of automobile are you riding home in? The random variable to be reported is the number of...
1. What view of the nature and origin of justice does Glaucon describe? 2. What does he try to show with the story of the ring of Gyges? 3. What does he want to demonstrate by imagining two people...
Which is not a physical property of a material? (a) Density (b) refractive index (c) Roughness (d) Thermal expansion
Coffey Corporation purchased debt investments for $52,000 on January 1, 2010. On July 1, 2010, Coffey received cash interest of $2,340. Journalize the purchase and the receipt of interest. Assume...
Explain the role of phase equilibrium thermodynamics in the design and optimization of liquid-liquid extraction systems, with a specific emphasis on tie-line data analysis and the prediction of phase...
Describe three specific programming situations that require a posttest loop.
With reference to Exercise 10.21, find the efficiency of the estimator of part (a) with Ï = 1/2 relative to this estimator with In exercise If 1 is the mean of a random sample of size n from a...
With reference to Exercise 10.23, find the efficiency of the estimator with = 1/2 relative to the estimator with = n 1 / n 1 + n 2 .
Use the data in MEAP00_01.RAW to answer this question. (i) Estimate the model mathA = (0 + (1 lunch + (2 log(enroll) + (3log(exppp) + u by OLS and obtain the usual standard errors and the fully...
ABC Co. purchased a used construction vehicle from another company that was liquidating its equipment. The purchase price was $150,000, and sales tax was 6%. The vehicle had to be transported to...
Apel Investment Company has GH41,800,000 of interest-bearing bond outstanding. The outstanding bonds have a 11% coupon and a 14% yield to maturity. Management believes they could issue new bonds at a...
Jasper Corp. has the following information available for 20X1: Description Amount Beginning Accounts Receivable account balance (Jan 1) $ 60,000 Credit sales during the year 1,500,000 Collections on...
A student takes on $40,000 of debt on August 2 of 2024 at an annual interest rate of 8%. She makes no payments while in school. On February 2, 2027 she prepares to start repaying her debt on a...
A company just starting a business purchased three inventory items at the following cost: March 2, $150; March 7, $160; and March 15, $180. If the company sold one unit for $230 on March 10 and one...
On January 1, 2025, Botosan Company issued a $1,200,000, 5-year, zero-interest-bearing note to National Organization Bank. The note was issued to yield 8% annual interest. Unfortunately, during 2026...
DC has unused FTC carryover from 2017 in the separate category for GC income as the result of income generated by a foreign branch. The income was foreign source general category income. In 2018 the...
Each month a brokerage house studies various companies and rates each companys stock as being either low risk or moderate to high risk. In a recent report, the brokerage house summarized its findings...
John and Jane are married. The probability that John watches a certain television show is .4. The probability that Jane watches the show is .5. The probability that John watches the show, given that...
In Exercise 4.20, find the probability that either John or Jane watches the show. In Exercise 4.20 John and Jane are married. The probability that John watches a certain television show is .4. The...
why you assume value of Machine A is assumed to decrease by $7,000 each year for the purpose of these calculations?
1. You want to create a Dog object. Which of the following would you use to describe it? (Choose all that apply.) A. String breed B. int age C. boolean isADog D. String ownerName E....
Part 1: Cathy Forth Photography Services (20 marks) You have been hired by Cathy Forth as her new bookkeeper. She has given you the following information: Use the current date and provide an...

If X 1 and X 2 are the means of independent random samples of sizes n 1

Question:

.X+(1-w) X2

Step by Step Answer:

var w 2 2 n 1 1 w 2 ...View the full answer

John E Freunds Mathematical Statistics With Applications

Students also viewed these Statistics questions