If the joint probability density of X and Y is given by Find the probability that the
Question:
If the joint probability density of X and Y is given by
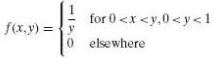
Transcribed Image Text:
0 elsewhere
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 70% (10 reviews)
12 dx dy dx d...View the full answer

Answered By

Branice Buyengo Ajevi
I have been teaching for the last 5 years which has strengthened my interaction with students of different level.
4.30+
1+ Reviews
10+ Question Solved
Related Book For 

John E Freunds Mathematical Statistics With Applications
ISBN: 9780134995373
8th Edition
Authors: Irwin Miller, Marylees Miller
Question Posted:
Students also viewed these Statistics questions
-
Use the known properties (i.e. domain, range, amplitude, period, etc.) of each function to sketch its graph for -2n sxs 2n 16. y = 2(cot x) - 3 17. y = -3 (csc 2x) 2 18. y = 2(sec 3x) 1 19. y = 2...
-
The joint density function of X and Y is given by f (x, y) = xex(y+1)x > 0, y > 0 (a) Find the conditional density of X, given Y = y, and that of Y, given X = x. (b) Find the density function of Z =...
-
The joint density function of X and Y is given by f(x, y) = 1/ye(y+x/y),x > 0, y > 0 Find E[X], E[Y], and show that Cov(X, Y) = 1.
-
List four components and four guidelines that the J. Crew mission statement fails to exhibit. Write a new and improved mission for J. Crew.
-
Refer to Applied Example 9.20, Ceramic Floor Tile, and Exercise 9.145 to continue the investigation of the floor tile manufacturing process. a. What are the assumptions for a chi-square test of...
-
Replace the force and couple moment system acting on the rectangular block by a wrench. Specify the magnitude of the force and couple moment of the wrench and where its line of action intersects the...
-
Consider the house price data in Table B.4. a. Fit a multiple regression model relating selling price to all nine regressors. b. Test for significance of regression. What conclusions can you draw? c....
-
On June 1, 2011, MacDougall Corporation approached Silverman Corporation about purchasing a parcel of undeveloped land. Silverman was asking $240,000 for the land and MacDougall saw that there was...
-
During 2021, Albert redeems Series EE savings bonds for $6,000 - - consisting of $2,000 interest and $4,000 principal. Albert has net qualifying education expenses of $5,000 in 2021. Albert, a single...
-
Consider a new design of a thermal reactor that requires square arrays of fuel rods. Heat is being generated uniformly along the fuel rods. Water and helium are being considered as single-phase...
-
If the joint probability density of X and Y is given by Find (a) P(X 1/2 , Y 1/2 ); (b) P(X + Y > 2/3 ); (c) P(X > 2Y). for y)-|2 elsewhere>Mr+ye!
-
Find the joint probability density of the two random variables X and Y whose joint distribution function is given by Fa.y)- elsewhere
-
Briefly describe the composition and general thrust of each of the following indexes. a.NYSE composite index b.Amex composite index c.Nasdaq Stock Market indexes d.Value Line composite index
-
Under the state code of your state, can licenses be revoked for the failure to pay child support? If so, what licenses? What are the conditions that will trigger a revocation?
-
One way to estimate narrow-sense heritability for a given trait is to compare __________ for _________. a. variances, related pairs of individuals b. correlation coefficients, related pairs of...
-
Kim lives in a house provided by her employer. The house cost her employer 246,500 in 2019 and a further 28,500 was spent on improvements in 2020. The house has a gross rateable value of 3,700 and it...
-
a. In your state code, find the statute that lists the grounds for divorce. Give the citation to this statute and list all the grounds for divorce provided therein. b. For each ground of divorce...
-
How long it will take to reduce the pressure of a 100 L tank from 1 Kg/cm2 (a) to 0.2 Kg/cm2 (a), if the pump capacity is 500 L/min. assume 10% leakage.
-
Solve each problem. varies jointly as h and the square of g, and f = 50 when h = 2 and g = 4. Find when h = 6 and g = 3.
-
Consider the reaction of acetic acid in water CH 3 CO 2 H(aq) + H 2 O(l) CH3CO 22 (aq) + H 3 O + (aq) where Ka 5 1.8 3 1025. a. Which two bases are competing for the proton? b. Which is the stronger...
-
There are three clues labeled daily double on the game show Jeopardy. If three equally matched contenders play, what is the probability that: a. A single contestant finds all three daily doubles? b....
-
Brooks Insurance Inc. wishes to offer life insurance to men age 60 via the Internet. Mortality tables indicate the likelihood of a 60-year-old man surviving another year is .98. If the policy is...
-
Forty percent of the homes constructed in the Quail Creek area include a security system. Three homes are selected at random: a. What is the probability all three of the selected homes have a...
-
Briefly define TinyOS and explain its goals as an embedded operating system.?
-
Consider the graph shown on the right. Find the strongly connected components of the graph. Whenever you use DFS and there is a choice of nodes to explore, always pick the one that is alphabetically...
-
After viewing the previous video, "Types of Operating Systems As Fast As Possible", explain the difference between embedded operating systems and desktop operating systems. (300-yep, you guessed it)...

Study smarter with the SolutionInn App


