If we assume in Example 9.8 that is a random variable having a uniform density with

Question:

If we assume in Example 9.8 that is a random variable having a uniform density with α = 0 and β = 1, show that the Bayes risk is given by

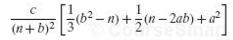
Also show that this Bayes risk is a minimum when a = 1 and b = 2, so that the optimum Bayes decision rule is given by d (x) = x+ 1 / n+ 2.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

John E Freunds Mathematical Statistics With Applications

ISBN: 9780134995373

8th Edition

Authors: Irwin Miller, Marylees Miller

See More Books

Question Posted: Nov 04, 2015 03:31 AM

See More Questions

In certain experiments, the error made in determining the density of a substance is a random variable having a uniform density with = 0.015 and = 0.015. Find the probabilities that such an error...
A single observation of a random variable having a uniform density with = 0 is used to test the null hypothesis = 0 against the alternative hypothesis = 0 + 2. If the null hypothesis is rejected...
The continuous random variable X has the beta distribution with parameters and 3 if its density function is given by where > 0 and > 0. If the proportion of a brand of television set requiring...
1. Rick and Barbara are married with two children. Four yearsago, Barbara bought a $75,000 life insurance policy on her motherslife and named her children as policy beneficiaries. Barbara didnot name...
As a quality-control inspector of toy trucks, you have observed that 3% of the time, the wooden wheels are bored off-center. If six wooden wheels are used on each toy truck, what is the probability...
Financial statements for Pal and Sun Corporations for 2011 are as follows (in thousands): ADDITIONAL INFORMATION 1. Pal acquired an 80 percent interest in Sun on January 2, 2009, for $290,000, when...
Search the Internet including social media to obtain information on flying and passengers' airline preferences. Develop three double-barreled questions related to flying and passengers' airline...
On July 23 of the current year, Dakota Mining Co. pays $4,836,000 for land estimated to contain 7,800,000 tons of recoverable ore. It installs machinery costing $390,000 that has a 10-year life and...
Warnerwoods Company uses a perpetual inventory system. It entered into the following purchases and sales transactions for March. Date Units Acquired at Cost: March 1 Activities Beginning inventory...
Reba Dixon is a fifth grade school teacher who earned a salary of $38,000 in 2014. She is 45 years old and has been divorced for four years. She received $1,200 of alimony payments each month from...
Find the value of that maximizes the risk function of Example 9.8, and then find the values of a and b that minimize the risk function for that value of . Compare the results with those given on...
Verify the results given on page 273 for the marginal density of X and the conditional density of given X = x.
The sample size formula for a confidence interval for the population mean requires an estimate of the population standard deviation. Intuitively, why is this the case? Specifically, why is the...
For the cooling tower described in Example 19.3, predict the effect of increasing the air rate by 20 percent with the same liquid rate and a wet-bulb temperature of 75F. Example 19.3 A counterflow...
Two identical 9. 60-g metal spheres (small enough to be treated as particles) are hung from separate $300-\mathrm{mm}$ strings attached to the same nail in a ceiling. Surplus electrons are added to...
Suppose two particles carry a positive charge of $1.00 \mathrm{C}$ for every kilogram of their mass. Compare the gravitational force and the electric force they exert on each other at a given...
You are an astrophysicist working on a problem involving Saturn's rings and trying to figure out why the smaller ice chunks in the rings stick to larger chunks. You hypothesize that as the chunks...
You have two rods A and B, both made of a nonconducting material. Initially, neither rod is charged. A sphere carrying 100 units of surplus positive charge is placed close to the left end of...
Write each number in standard notation. -7.68 10 -4
You have accepted the engagement of auditing the financial statements of the C. Reis Company, a small manufacturing firm that has been your auditee for several years. Because you were busy writing...
Find the numerical values of a. b. P 5 2 c. P 4 2 d. e. f. g. P 5 3 h. P 10 0 9. 3,
Determine the number of sample points contained in the sample space when you toss the following: a. 1 die b. 2 dice c. 4 dice d. n dice
Refer to the American Journal of Physical Anthropology (Vol. 142, 2010) study of the dietary habits of extinct mammals, Exercise. Recall that 18 cheek teeth extracted from skulls of an extinct...
Imagine yourself at a fair playing one of the midway games. Pick a game and calculate the expected value and post your results along with how you calculated them.
1. What is the ratio of 2 lengths which are 25 cm and 7.5 m respectively?
If f(x, t) does not depend on x, then we have x' = f(t), so that x(t) = (0 to t) f(u)du. Show that, in this case, the RK4 algorithm reduces to Simpson's rule.

If we assume in Example 9.8 that is a random variable having a uniform density with

Question:

-)+국(n-2ab)+a (n+ b)?

Step by Step Answer:

Substituting into R d yields Differentiating par...View the full answer

John E Freunds Mathematical Statistics With Applications

Students also viewed these Statistics questions