In a certain city the daily consumption of water (in millions of liters) is a random variable

Question:

In a certain city the daily consumption of water (in millions of liters) is a random variable whose probability density is given by

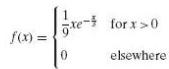
What are the probabilities that on a given day

(a) The water consumption in this city is no more than 6 million liters;

(b) The water supply is inadequate if the daily capacity of this city is 9 million liters?

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

John E Freunds Mathematical Statistics With Applications

ISBN: 9780134995373

8th Edition

Authors: Irwin Miller, Marylees Miller

See More Books

Question Posted: Nov 04, 2015 03:05 AM

See More Questions

In a certain city, the daily consumption of water (in millions of liters) follows approximately a gamma distribution with Q = 2 and = 3. If the daily capacity of that city is 9 million liters of...
In a certain city the temperature (in F) hours after 9 A.M. was modeled by the function Find the average temperature during the period from 9 A.M. to 9 P.M. T() - 50 + 14 sin 12
In a certain city the temperature (in oF) hours after 9 AM was modeled by the function T(t) = 50 + 14 sin t/12 Find the average temperature during the period from 9 AM to 9 PM.
A quality of information demonstrated when different independent observers could reach the same general conclusions that the information represents what it purports to represent is: O a...
Find the values of t that bound the middle 0.95 of the distribution for df = 12.
The internal drag truss for the wing of a light airplane is subjected to the forces shown. Determine the force in members BC, BH, and HC, and state if the members are in tension orcompression. H. -2...
Chemical and mechanical engineers often need to know the vapor pressure of water at various temperatures (the "infamous" steam tables can be used for this). Below are data on the vapor pressure of...
Discuss the accuracy of this statement: Formal strategic planning systems are irrelevant for firms competing in high- technology industries where the pace of change is so rapid that plans are...
Zamphir Jets manufactures luxury jets for corporate use. Its main production line is devoted to manufacturing the Z 1 jet, which is its standardized product offering. At any point in time, 2 0 to 3 0...
Armco, Inc., is a manufacturing company that has a contract to supply a customer with parts from April through September. However, Armco does not have enough storage space to store the parts during...
The total lifetime (in years) of five- year- old dogs of a certain breed is a random variable whose distribution function is given by Find the probabilities that such a five- year- old dog will live...
Two textbooks are selected at random from a shelf that contains three statistics texts, two mathematics texts, and three physics texts. If X is the number of statistics texts and Y the number of...
A spherical gel capsule of 0.50 cm diameter is used a drug delivery device. Initially, there is a total drug amount 0.005 mmole uniformly loaded into the gel material. The capsule is ingested, and...
Does group decision-making influence individual behavior?
Which kind of gateways does BPMN have, and which are their purpose?
Which of these refers to the extent to which members interacting with each other in the group are influenced by the thought process of the members within the group? Role ambiguity Role conflict ...
Distinguish between realty and personalty.
Expectations between an individual and the organization on the whole, which are not defined but which will influence the motivation to work, are: The psychological aspect The sociological aspect ...
The equity sections from the 2023 and 2024 balance sheets of Fab-Form Industries Inc. appeared as follows: On March 16, June 15, September 5, and November 22, 2021, the board of directors declared...
(a) Find the equation of the tangent line to f(x) = x 3 at the point where x = 2. (b) Graph the tangent line and the function on the same axes. If the tangent line is used to estimate values of the...
Shortys Muffler advertises it can install a new muffler in 30 minutes or less. However, the work standards department at corporate headquarters recently conducted a study and found that 20% of the...
A study conducted by the nationally known Taurus Health Club revealed that 30% of its new members are 15 pounds overweight. A membership drive in a metropolitan area resulted in 500 new members. a....
A recent issue of Bride Magazine suggested that couples planning their wedding should expect two-thirds of those who are sent an invitation to respond that they will attend. Rich and Stacy are...
Estimate the final temperature in Celsius of the combination if I drop 5 rolls of pennies at 2 0 C ( each roll is 5 0 pennies stacked together; assume they are pure copper ) into a cup of recently -...
A 100 gram mass is hung of then end of a cantilever beam . The beam is made of brass, and is 30 cm long (), 2 cm wide, and 3 mm thick. Find the resulting deflection ()
The nitrogen-vacancy (NV) and silicon-vacancy (SiV) defects in diamond can lead to many exciting quantum nanotechnologies in physical and biological sciences, including single-photon sensors,...

In a certain city the daily consumption of water (in millions of liters) is a random variable

Question:

for x > 0 elsewhere jxe_, f(x)=

Step by Step Answer:

a F6 1 3e 2 1 3e 2 1 3...View the full answer

John E Freunds Mathematical Statistics With Applications

Related Video

Students also viewed these Statistics questions