In a certain contest, the players are of equal skill and the probability is 1/2 that a specified one of the two contestants will be the victor. In a group of 2ⁿ players, the players are paired off against each other at random. The 2ⁿ⁻¹ winners are again paired off randomly, and so on, until a single winner remains. Consider two specified contestants, A and B, and define the events A_i, i ≤ n, E by

A_i: A plays in exactly i contests:

E: A and B never play each other.

(a) Find P(A_i), i = 1, . . . , n.

(b) Find P(E).

(c) Let P_n = P(E). Show that

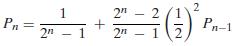
and use this formula to check the answer you obtained in part (b).

Find P(E) by conditioning on which of the events A_i, i = 1, . . . , n occur. In simplifying your answer, use the algebraic identity

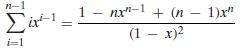
For another approach to solving this problem, note that there are a total of 2ⁿ − 1 games played.

(d) Explain why 2ⁿ − 1 games are played. Number these games, and let B_i denote the event that A and B play each other in game i, i = 1, . . . , 2ⁿ − 1.

(e) What is P(B_i)?

(f) Use part (e) to find P(E).

Transcribed Image Text:

2"2 1 n-1 (1 - x)2 i-1