In his analysis of Californias Proposition 103 (see Illustration 4.2), Benjamin Zycher notes that one of the
Question:
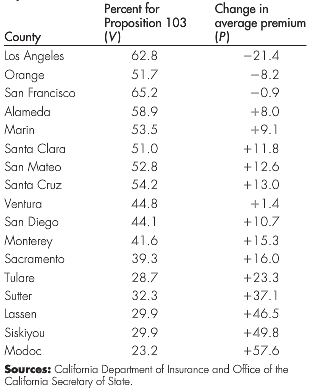
In his analysis of California’s Proposition 103 (see Illustration 4.2), Benjamin Zycher notes that one of the most important provisions of this proposition is eliminating the practice by insurance companies of basing premiums (in part) on the geographic location of drivers. Prohibiting the use of geographic location to assess the risk of a driver creates a substantial implicit subsidy from low-loss counties to high-loss counties, such as Los Angeles, Orange, and San Francisco counties. Zycher hypothesizes that the percent of voters favoring Proposition 103 in a given county (V) is inversely related to the (average) percentage change in auto premiums (P) that the proposition confers upon the drivers of that county.
The data in the table below were presented by Zycher to support his contention that V and P are inversely related:
Using the data in the table, we estimated the regression equation
V = a + bP
to see if voting behavior is related to the change in auto insurance premiums in a statistically significant way. Here is the regression output from the computer:
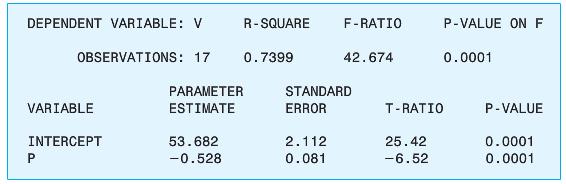
a. Does this regression equation provide evidence of a statistically significant relation between voter support for Proposition 103 in a county and changes in average auto premiums affected by Proposition 103 in that county? Perform an F-test at the 95 percent level of confidence.
b. Test the intercept estimate for significance at the 95 percent confidence level. If Proposition 103 has no impact on auto insurance premiums in any given county, what percent of voters do you expect will vote for the proposition?
c. Test the slope estimate for significance at the 95 percent confidence level. If P in-creases by 10 percent, by what percent does the vote for Proposition 103decline?
Step by Step Answer:

Managerial Economics Foundations of Business Analysis and Strategy
ISBN: 978-0078021718
11th edition
Authors: Christopher Thomas, S. Charles Maurice





