In this exercise, you will prove that, as long as tastes satisfy rationality, continuity and monotoni city,

Question:

In this exercise, you will prove that, as long as tastes satisfy rationality, continuity and monotoni city, there always exists a well-defined indifference map (and utility function) that can represent those tastes.2

A: Consider a 2-good world, with goods x₁ and x₂ represented on the two axes in any graphs you draw.

(a) Draw your two axes and pick some arbitrary bundle 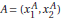A= (x4.x4) that contains at least some of each good.

(b) Draw the 45-degree line in your graph €” this is a ray that represents all bundles that have equal amounts of x₁ and x₂ in them.

(c) Pick a second bundle B = 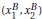In this exercise, you will prove that, as long as such that 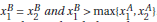In other words, pick B such that it has equal amounts of x₁ and x₂ and such that it has more of x₁ and x₂ than A.

(d) Is A more or less preferred than the bundle (0,0)? Is B more or less preferred than A?

(e) Now imagine moving along the 45-degree line from(0,0) toward B. Can you use the continuity property of tastes we have assumed to conclude that there exists some bundle C between (0,0) and B such that the consumer is indifferent between A and C?

(f) Does the same logic imply that there exists such an indifferent bundle along any ray from the origin and not just along the 45-degree line?

(g) How does what you have just done demonstrate the existence of a well-defined indifference map?

B: Next we show that the same logic implies that there exists a utility function that represents these tastes.

(a) If you have not already done so, illustrate A(a)-(e).

(b) Denote the distance from (0,0) to C on the 45-degree line as In this exercise, you will prove that, as long as and assign the value t^A to the bundle A.

(c) Imagine the same procedure for labeling each bundle in your graph €” i.e. for each bundle, determine what bundle on the 45-degree line is indifferent and label the bundle with the distance on the 45-degree line from (0,0) to the indifferent bundle. The result is a function u(x₁,x₂) that assigns to every bundle a number. Can you explain how this function meets our definition of a utility function?

(d) Can you see how the same method of proof would work to prove the existence of a utility function when there are more than 2 goods (and when tastes satisfy rationality, continuity and monotonicity)?

(e) Could we have picked a ray other than the 45-degree line to construct the utility values associated with each bundle?