Independent trials that result in a success with probability p and a failure with probability 1
Question:
Independent trials that result in a success with probability p and a failure with probability 1 − p are called Bernoulli trials. Let Pn denote the probability that n Bernoulli trials result in an even number of successes (0 being considered an even number). Show that
Pn = p(1 − Pn−1) + (1 − p)Pn−1 n ≥ 1
and use this formula to prove (by induction) that
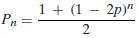
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





