Let H k (n) be the number of vectors x 1 , , x k for which each x i is a positive integer satisfying 1 x i n and x 1 x 2 x k (a) Without any computations, argue that H 1 (n) n How many vectors are there in which x k j (b) Use the preceding recursion to compute H 3 (5) First compute H 2 (n) for n 1,...

a The number of vectors that have x k j is equal to the number of vectors x 1 ...

Let H k (n) be the number of vectors x 1 , . . ., x k

Question:

Let H_k(n) be the number of vectors x₁, . . ., x_k for which each x_i is a positive integer satisfying 1 ≤ x_i ≤ n and x₁ ≤ x₂ ≤ . . . ≤ x_k.

(a) Without any computations, argue that H₁(n) = n

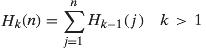
How many vectors are there in which x_k = j?

(b) Use the preceding recursion to compute H₃(5).

First compute H₂(n) for n = 1, 2, 3, 4, 5.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

A First Course In Probability

ISBN: 9789332519077

9th Edition

Authors: Sheldon Ross

See More Books

Question Posted: Oct 22, 2015 02:43 AM

See More Questions

Determine the number of vectors (x1, . . ., xn) such that each xi is a nonnegative integer and k i=1
Determine the number of vectors (x1, . . ., xn), such that each xi is either 0 or 1 and X 2 k i=1
Suppose we wish to estimate the probability, PA, of some event, A . We do so by repeating an experiment n times and observing whether or not the event A occurs during each experiment. In particular,...
4. Papo and Pepe are two barbers from a small barbershop. Theyhave their two court chairs plus two waiting chairs. The followingresults were found: P0 = 1/16 P1 = 4/16 P2 = 6/16 P3 = 4/16 a. What is...
Natural History magazine has published a listing of the maximum speeds (in mph) for a wide variety of animals, including those shown in the table. a. Determine the mean and the median for these data....
Consider a room that is initially at the outdoor temperature of 20C. The room contains a 100-W lightbulb, a 110-W TV set, a 200-W refrigerator, and a 1000-W iron. Assuming no heat transfer through...
Fitted Values. Let \(\left.\widehat{y}_{i}=\pi\left(\mathbf{x}_{i}^{\prime} \mathbf{b}_{M L E} ight) ight)\) denote the \(i\) th fitted value for the logit function. Assume that an intercept is used...
The required steps in the accounting cycle are listed in random order below. List the steps in proper sequence. (a) Prepare a post-closing trial balance. (b) Prepare an adjusted trial balance. (c)...
You are required to configure a LINUX-based web server with the following basic requirements: Demonstrate virtual hosting (i.e. your server must be able to serve at least two different websites using...
Layla Bright has run a bicycle shop for several years in rented shop premises. She sells new and reconditioned second-hand bikes and runs a repair service, with the help of a part-time assistant. The...
From a set of n people, a committee of size j is to be chosen, and from this committee, a subcommittee of size i, i j, is also to be chosen. (a) Derive a combinatorial identity by computing, in two...
Consider a tournament of n contestants in which the outcome is an ordering of these contestants, with ties allowed. That is, the outcome partitions the players into groups, with the first group...
Calcium carbide, CaC 2 , contains the acetylide ion, C 2 2 . Sketch the molecular orbital energy level diagram for the ion and the electron dot structure. (a) How many net and bonds does the ion...
Using Gauss elimination, solve the following linear algebraic equations: \[ \begin{aligned} -25 x_{1}+10 x_{2}+10 x_{3}+10 x_{4} & =0 \\ 5 x_{1}-10 x_{2}+10 x_{3} & =2 \\ 10 x_{1}+5 x_{2}-10 x_{3}+10...
Which statement is true? a) Most of the largest corporate mergers in our history took place during the period 19982000. b) There have been virtually no large mergers in banking or communications. c)...
The MRP of the fourth unit of output is equal to the _____________ less the ___________.
A firm will keep hiring more and more of a resource up to the point at which its MRP is equal to __________. a) one b) its marginal physical product c) its price d) its output
The producers surplus of rented land is the difference between how much this land is __________ and how much _________________.
In Exercises 4170, use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. Where possible, evaluate logarithmic...
You continue to work in the corporate office for a nationwide convenience store franchise that operates nearly 10,000 stores. The per- store daily customer count (i.e., the mean number of customers...
A bag contains white and black balls. Balls are chosen from the bag according to the following method: A. A ball is chosen at random and is discarded. B. A second ball is then chosen. If its color is...
Consider the gamblers ruin problem, with the exception that A and B agree to play no more than games. Let P n,i denote the probability that A winds up with all the money when starts with i and B...
Let Q n denote the probability that no run of 3 consecutive heads appears in n tosses of a fair coin. Show that Find Q 8 . 1 1 +-Qn-2 +3 en-3 1 2 n-1 Q1 = Q2 = 1
It is March, and the annual NCAA Basketball Tournament is down to the final 4 teams. Randy Kitchell is a t-shirt vendor who plans to order t-shirts with the names of the final 4 teams from a...
L = {w| L2 = {w| Two languages L1 and L2 are defined by symbols = {0, 1}, written as w contains 00 as a sub-string and the length of w is even number} w begins with 0 and ends with 1} (i) Write two...
a. Write a story problem for the expression 6 x b. Find the value of the expression. Show or explain your work. da f

Let H k (n) be the number of vectors x 1 , . . ., x k

Question:

Hа (n) 3D Н-10) k> 1 =1

Step by Step Answer:

a The number of vectors that have x k j is equal to the number of vectors x 1 ...View the full answer

A First Course In Probability

Students also viewed these Statistics questions