Let X 1 and X 2 constitute a random sample of size 2 from the population given by If the critical region x 1 x 2 3 4 is used to test the null hypothesis 1 against the alternative hypothesis 2, what is the power of this test at 2 9for0...

Let X 1 and X 2 constitute a random sample of size 2 from the population given

Question:

Let X₁ and X₂ constitute a random sample of size 2 from the population given by

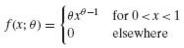
If the critical region x₁x₂ ≥ 3/4 is used to test the null hypothesis θ = 1 against the alternative hypothesis θ = 2, what is the power of this test at θ = 2?

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

John E Freunds Mathematical Statistics With Applications

ISBN: 9780134995373

8th Edition

Authors: Irwin Miller, Marylees Miller

See More Books

Question Posted: Nov 04, 2015 03:40 AM

See More Questions

If X 1 and X 2 constitute a random sample of size n = 2 from an exponential population, find the efficiency of 2Y 1 relative to X, where Y 1 is the first order statistic and 2Y 1 and X are both...
If X1 and X2 constitute a random sample of size n = 2 from a Poisson population, show that the mean of the sample is a sufficient estimator of the parameter .
Let X 1 and X 2 constitute a random sample from a normal population with 2 = 1. If the null hypothesis = 0 is to be rejected in favor of the alternative hypothesis = 1 > 0 when > 0 + 1, what...
Someone offered the investment options to Hendry on January 1, 2023: 1. Hendry has to save up to 5 times the initial deposit of US $ 150,000/year. 2. The savings cannot be taken for 20 years until...
Show that if event A is a subset of event B, then P(A or B) =P(B).
1. How would you classify Lugars startup idea? Is it a new market idea, new technology idea, or new benefit idea? 2. What was the source of Lugars startup idea? 3. Would you recommend that he give...
A surface condenser is a (a) water tube device (b) steam tube device (c) steam and cooling water mix to give the condensate (d) all of the above
The PDC Company was described earlier in this chapter. Refer to the PDC Companys projected monthly operating schedules in Table 6.2. PDCs sales are projected to be $80,000 in September 2011. A....
What are the key challenges in using advanced absorbents, like metal-organic frameworks (MOFs) or zeolites, in gas-phase absorption processes? Discuss their impact on capacity, selectivity, and...
Hawaii sugar company produces brown sugar, white sugar, powdered sugar and molasses from sugar cane syrup. the company purchases 4000 tons of syrup weekly and is contracted to deliver at least 25...
A single observation of a random variable having a uniform density with = 0 is used to test the null hypothesis = 0 against the alternative hypothesis = 0 + 2. If the null hypothesis is rejected...
Given a random sample of size n from a normal population with the known variance 2, show that the null hypothesis = 0 can be tested against the alternative hypothesis 0 with the use of a one-...
Consider the situation of Example 10.6.2. (a) Verify that IF(, x) = x - Î¼. (b) For the median we have T(F) = m if P(X ¤ m) = 1/2 or m = F-1(1/2). If X ~ F6, show that and thus...
Chanterelle Inc. acquired 30% interest, or 1,200 common shares, of Cedar Inc. on January 1, 2021. Chanterelle Inc. paid $45 per share. At that time, the carrying amount of Cedar Inc.'s net assets was...
Find x, y, z using Cramer's rule: 2x+3y+5z = 10 3x + 7y+4z = 3 x+2y+22=3
Solve the following equation by factoring. Solve for zero first. x - 3x 3x18
2. Write a program in assembly language to check whether a number is prime or not. a. Use that program to determine number 31 is prime or not. b. Repeat the same program with 189 and 223.
Drone Berhad wants to do a stock split of 5 to 1. Given below is the partial equity account for Drone Berhad: Partial Equity Account for Drone Berhad (RM) Common Stock @ RM2 Premium Retained Earnings...
In Exercises 21 through 34, either evaluate the given improper integral or show that it diverges. L -00 ,2x 1 (x - 1) dx
Before the latest financial crisis and recession, when was the largest recession of the past 50 years, and what was the cumulative loss in output over the course of the slowdown?
You plan to sample and test units from a recently assembled order of Bluetooth mobile speakers. How many different samples (combinations) are possible if you plan to sample a. 3 units from an order...
Twelve players are waiting on the sidelines to play pick-up basketball at Penwell Gym. Five players are needed to play the winners of the game currently in progress. a. How many different teams...
You intend to study consumer trends in six countries in Europe and Asia. You have narrowed your list of possibilities to a total of 15 countries10 in Europe and 5 in Asia. From this list, you plan to...
explain and comments thies pints Has existed for a long time One of the original fast-food establishments High standing Commonly recognized for its root beer. With high-quality cuisine Markets to...
12 Stiler XYZ currently has an enterprise value of $600 million, 20 million shares outstanding, $200 million in excess cash and no debt. Assuming XYZ uses its excess cash to repurchase shares, and...
Explain a summary of the news story in the link below. Your summary should include at least 3 of the marketing concepts learned to date in this course. Be sure to include an accurate, succinct...

Let X 1 and X 2 constitute a random sample of size 2 from the population given

Question:

9for0

Step by Step Answer:

1B 4 x x dx dx xj 34 3...View the full answer

John E Freunds Mathematical Statistics With Applications

Students also viewed these Statistics questions