Show that if a random variable has the probability density f(x) = 1/2 e|x| for <
Question:
Show that if a random variable has the probability density
f(x) = 1/2 e–|x| for –∞ < x < ∞
Its moment-generating function is given by
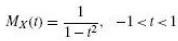
Transcribed Image Text:
Mx(t) = -1
Mx(t) = -1
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 85% (7 reviews)
ee dx ee dx y x cy d...View the full answer

Answered By

Asim farooq
I have done MS finance and expertise in the field of Accounting, finance, cost accounting, security analysis and portfolio management and management, MS office is at my fingertips, I want my client to take advantage of my practical knowledge. I have been mentoring my client on a freelancer website from last two years, Currently I am working in Telecom company as a financial analyst and before that working as an accountant with Pepsi for one year. I also join a nonprofit organization as a finance assistant to my job duties are making payment to client after tax calculation, I have started my professional career from teaching I was teaching to a master's level student for two years in the evening.
My Expert Service
Financial accounting, Financial management, Cost accounting, Human resource management, Business communication and report writing. Financial accounting : • Journal entries • Financial statements including balance sheet, Profit & Loss account, Cash flow statement • Adjustment entries • Ratio analysis • Accounting concepts • Single entry accounting • Double entry accounting • Bills of exchange • Bank reconciliation statements Cost accounting : • Budgeting • Job order costing • Process costing • Cost of goods sold Financial management : • Capital budgeting • Net Present Value (NPV) • Internal Rate of Return (IRR) • Payback period • Discounted cash flows • Financial analysis • Capital assets pricing model • Simple interest, Compound interest & annuities
4.40+
65+ Reviews
86+ Question Solved
Related Book For 

John E Freunds Mathematical Statistics With Applications
ISBN: 9780134995373
8th Edition
Authors: Irwin Miller, Marylees Miller
Question Posted:
Students also viewed these Statistics questions
-
Show that if a random variable has an exponential density with the parameter , the probability that it will take on a value less than ln(1 ) is equal to p for 0 p < 1.
-
Show that if a random variable has a uniform density with the parameters and , the rth moment about the mean equals (a) 0 when r is odd; (b) 1 / r + 1 ( / 2)r when r is even.
-
A random variable has the following density function. f(x) = 1 .5x 0 < x < 2 a. Graph the density function. b. Verify that f(x) is a density function. c. Find P(X > 1). d. Find P(X < .5). e. Find...
-
In 2020, A corporation gave the following fringe benefits to its employees (Non-resident alien not engaged in trade/business): To managerial employees - P1,500,000 To rank and file employees -...
-
a. Find a, the probability of the type I error. b. Find b, the probability of the type II error.
-
Determine the placement a of the roller support B so that the maximum moment within the span AB is equivalent to the moment at the supportB. Wo L-
-
Using the gasoline mileage data in Table B. 3 find the eigenvectors associated with the smallest eigenvalues of \(\mathbf{X}^{\prime} \mathbf{X}\). Interpret the elements of these vectors. What can...
-
Jake Tweet hosts a psychology talk show on KRAN radio. Jakes advice averages 10 minutes per caller but varies according to an exponential distribution. The average time between calls is 25 minutes,...
-
Pharoah Industries produces and sells a cell phone-operated home security control systems. Information regarding the costs and sales during May 2022 is as follows. Unit selling price $45.00 Unit...
-
Complete Keith's tax return including all required schedules and forms using prince edward island as province, using the fillable forms package. Taxpayers Information Taxpayer #1 Name: Keith Dox...
-
If we let RX(t) = lnMX(t), show that R'X(0) = and R''X(0) = 2. Also, use these results to find the mean and the variance of a random variable X having the moment- generating function MX(t) = e4(e4 ...
-
With reference to Exercise 4.37, find the variance of the random variable by In exercise (a) Expanding the moment-generating function as an infinite series and reading off the necessary coefficients;...
-
What was the Michelson-Morley experiment designed to detect? Why did they expect that the speed of light might vary at different times of the year? Explain.
-
Williams entered a Walmart nine times in 27 hours to buy multiple cans of dust remover on each visit. Employees noticed bad behavior by her while in the store, and she said on one visit that she had...
-
McGrory worked for Applied Signal Technology in a supervisory position. He was accused of violating the companys policies on sexual harassment. An internal investigation determined he did not violate...
-
A police officer was served a hamburger at a Burger King at the checkout window. Thinking something was not right, he took off the top bun and saw that an employee had spit on the burger, which was...
-
Two boys were unattended by their father in a store. They took bicycles from the rack and rode them around in the store. One crashed and required stitches in his leg. His parents sued for premises...
-
TripAdvisor publishes information about hotels. It listed Grand Resort Hotel in Pigeon Forge, Tennessee, as one of the dirtiest hotels in the country. The owner of the hotel sued for false-light...
-
To solve the equation rp - rq = p + q for r, a student began by adding rq and then dividing by p to obtain Give the correct answer. r= p+q+rq P
-
Fill in each blank so that the resulting statement is true. A solution to a system of linear equations in two variables is an ordered pair that__________ .
-
Apple products have become a household name in America with 51 percent of all households owning at least one Apple product (CNN, March 19, 2012). The likelihood of owning an Apple product is 61...
-
According to the Censuss Population Survey, the percentage of children with two parents at home is the highest for Asians and lowest for blacks (USA TODAY, February 26, 2009). It is reported that 85%...
-
Christine Wong has asked Dave and Mike to help her move into a new apartment on Sunday morning. She has asked them both in case one of them does not show up. From past experience, Christine knows...
-
Assume that a robot systems constant failure and repair rates are 0.0004 failures per hour and 0.002 repairs per hour, respectively. Calculate the robot system steady-state unavailability and...
-
March 6, 2018 David Beckham's Latest Pitch: Men's Cosmetics. By Robert Williams Men of the world, David Beckham has a message for you: Moisturize. "It's the biggest thing," he says in a London...
-
3. On January 1, an investment fund was opened with an initial balance of 5000. Just after the balance grew to 5200 on July 1, an additional 2600 was deposited. The annual effective yield rate for...

Study smarter with the SolutionInn App


