Show that for a finite group, every refinement of a subnormal series with abelian quotients also has
Question:
Show that for a finite group, every refinement of a subnormal series with abelian quotients also has abelian quotients, thus completing the proof of Lemma 56.3.
Data from Lemma 56.3
Let F be a field of characteristic 0, and let a ∈ F. If K is the splitting field of xn - a over F, then G(K / F) is a solvable group.
Proof Suppose first that F contains all the nth roots of unity. By Corollary 23.6 the nth roots of unity form a cyclic subgroup of (F*, ·). Let ζ be a generator of the subgroup. (Actually, the generators are exactly the primitive nth roots of unity.) Then the nth roots of unity are
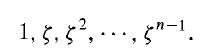
If β ∈ F̅' is a zero of (xn - a) E F[x], then all zeros of xn - a are
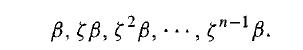
Since K = F(β), an automorphism a in G(K/F) is determined by the value σ(β) of the automorphism σ on β. Now if σ(β) = ζi β and τ(β) = ζj β, where τ ∈ G(K/F), then
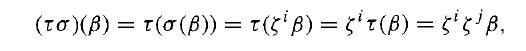
since ζi ∈ F. Similarly,
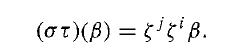
Thus στ = τσ, and G(K/F) is abelian and therefore solvable.
Now suppose that F does not contain a primitive nth root of unity. Let ζ be a generator
of the cyclic group of nth roots of unity under multiplication in F̅. Let β again be a zero
of xn - a. Since β and ζβ are both in the splitting field K of xn - a, ζ = (ζβ)/β is in K. Let F' = F(ζ), so we have F < F' ≤ K. Now F' is a normal extension of F, since F' is the splitting field of xn - 1. Since F' = F(ζ), an automorphism η in G(F'/F) is determined by n(ζ), and we must have n(ζ) = ζi for some i, since all zeros of xn - 1 are powers of ζ. If μ(ζ) = ζj for μ ∈ G(F'/F), then
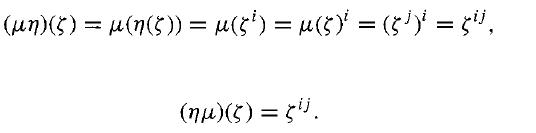
Thus G(F'/F) is abelian. By the Main Theorem of Galois Theory,
is a normal series and hence a subnormal series of groups. The first part of the proof shows that G(K/F') is abelian, and Galois theory tells us that G(K/F)/G(K/F') is isomorphic to G(F'/F), which is abelian. Exercise 6 shows that if a group has a subnormal series of subgroups with abelian quotient groups, then any refinement of this series also has abelian quotient groups. Thus a composition series of G(K/F) must have abelian quotient groups, so G(K/F) is solvable.
Step by Step Answer:
We can achieve any refinement of a subnormal series by insertin...View the full answer
