For any homomorphism f : A - B of left R-modules the diagram is commutative, where θ_A,θ_B are as in Theorem 4.12 and ∫* is the map induced on A** = Hom_R(Hom_R(A,R),R) by the map ∫̅: Hom_R(B,R) - Hom_R(A,R). 

Data from theorem 4.12

Let A be a left module over a ring R.

(i) There is an R-module homomorphism θ: A→A**.

(ii) i∫ R has an identity and A is free, then θ is a monomorphism.

(iii) i∫ R has an identity and A is free with a finite basis, then θ is an isomorphism. A module A such that θ: A → A** is an isomorphism is said to be reflexive.

PROOF OF 4.12.

(i) For each a ϵ A let θ(a): A* → R be the map defined by [θ(a)](∫) = (a,∫) ϵ R. Statement (2) after Theorem 4.10 shows that θ(a) is a homomorphism of right R-modules (that is, θ(a) ϵ A**). The map θ: A → A** given by a|→ θ(a) is a left R-module homomorphism by (1) after Theorem 4.10.

(ii) Let X be a basis of A. If a ϵ A, then a = r₁x₁ + r₂x₂ + · · · + r_nx_n (r_i ϵ R; X_i ϵ X). If θ(a) = 0, then for all ∫ ϵ A*, 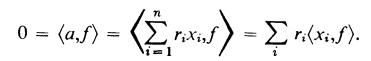In particular, for ∫= ∫_xj (j = 1,2, ... , n), 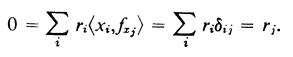Therefore, and θ is a monomorphism.

(iii) If X is a finite basis of A, then A* is free on the (finite) dual basis {∫_x Ix ϵ X} by Theorem 4.11. Similarly A** is free on the (finite) dual basis {g_x Ix ϵ X}, where for each x ϵ X, g_x: A* → R is the homomorphism that is uniquely determined by the condition: gx(∫_y) = δ_xy (y ϵ X). But θ(x) ϵ A** is a homomorphism A* → R such that for every y ϵ X Hence g_x = θ(x) and {θ(x) Ix ϵ X} is a basis of A**. This implies that Im θ = A**, whence θ is an epimorphism. 

Transcribed Image Text:

A B ОА B *** В**