For extraction of benzoic acid from water into toluene with toluene the dispersed phase, we measure the following mole fractions of benzoic acid: \(\mathrm{x}_{\mathrm{D}, \text { in }}=0, \mathrm{x}_{\mathrm{D}, \text { out }}=0.00023\), and \(\mathrm{x}_{\mathrm{C}, \text { out }}=1.99 \times 10^{-6}\). The mixer is \(0.75 \mathrm{~m}\) tall and has a \(0.75 \mathrm{~m}\) diameter. Flow rate of the dispersed phase is \(\mathrm{Q}_{\mathrm{D}}=0.0012 \mathrm{~m}^{3} / \mathrm{s}\) and \(\mathrm{Q}_{\mathrm{C}}=0.097 \mathrm{~m}^{3} / \mathrm{s}\). Data for density, equilibrium, and molecular weight are in Example 16-5.

a. Determine stage efficiency \(\mathrm{E}_{\mathrm{MD}, \text { mole_frac }}\). Note: The unit conversion in Eq. (16-94) is required to calculate \(\mathrm{m}\) for equilibrium, \(\mathrm{y}=\mathrm{mx}\), in mole fractions.

Eq.16-94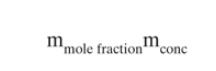
b. Calculate value of \(\mathrm{K}_{\mathrm{O}-\mathrm{ED}} \mathrm{a}\) using the completely mixed staged model.
c. Calculate value of \(\mathrm{K}_{\mathrm{O}-\mathrm{ED}} \mathrm{a}\) using the differential equation model.

d. If by accident the value of K_O−EDa calculated using the completely mixed staged model is used to predict the stage efficiency using the differential equation model, what (incorrect) value of E_{MD,mole_frac} is obtained?

Transcribed Image Text:

= Treybal (1980) estimates the overall mass transfer coefficient and stage efficiency for a mixer (0.5-m high and 0.5-m diameter, Amixer = 0.1963 m, Vmixer = 0.09817 m) extracting benzoic acid from water into pure toluene solvent. The water plus benzoic acid flow rate is QF = 0.003 m/s, and toluene flow rate is Qp = 0.0003 m/s. The tank is well mixed. Toluene is dispersed, and QD is estimated as 0.0824. The estimated dispersed-phase surface to volume ratio ap 1940.0 m dispersed phase/m dispersed phase. The estimated overall dispersed-phase mass transfer coefficient KLD = 2.01 x 10-5 kmol benzoic/[ms(kmol benzoic/m)]. Additional data: Ptoluene = 865 kg/m, MW toluene = 92.14 kg/kmol. Equilibrium is Cextract = 20.8 Craffinate (Cextract is kmol benzoic/m extract); since solvent is the dispersed phase, McD = 1/20.8 = 0.0481 [see Eq. (16-80c analog) listed in the solution to part a]. A. Convert the mass transfer coefficient to the units used in this section. B. Calculate the stage efficiency using the completely mixed model. C. Calculate the stage efficiency using the differential equation approach. D. Calculate the exiting raffinate and extract mole fractions for a completely stirred mixer if entering solvent contains no benzoic acid and entering feed is 0.03 mol% benzoic acid in water.