The Laplacian of a scalar is important in mass and heat transfer applications, and is obtained by
Question:
The Laplacian of a scalar is important in mass and heat transfer applications, and is obtained by applying the operator \(abla \cdot\) the gradient of a scalar, e.g., to \(abla T\). By applying this to Eq. (1.15) verify that the Laplacian in Cartesian coordinates is given by
\[\begin{equation*}abla \cdot abla T=abla^{2} T=\frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}+\frac{\partial^{2} T}{\partial z^{2}} \tag{1.56}\end{equation*}\]
Derive the following corresponding expression for the cylindrical coordinates
\[\begin{equation*}abla^{2} T=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial T}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} T}{\partial \theta^{2}}+\frac{\partial^{2} T}{\partial z^{2}} \tag{1.57}\end{equation*}\]
What is the form of these expressions if the temperature is a function of \(r\) only?
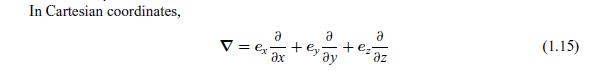
Step by Step Answer:

Advanced Transport Phenomena Analysis Modeling And Computations
ISBN: 9780521762618
1st Edition
Authors: P. A. Ramachandran





