To provide a simplified calculation method for the variable flow rate leaching problem solved in Example 14-2, your boss asks you to force-fit the problem so that a Kremser equation solution can be obtained. To do this, define a constant flow rate of the meal, \(\mathrm{F}_{\mathrm{M}}=800.0 \mathrm{~kg} \mathrm{meal} / \mathrm{h}\), and a constant solvent flow rate, \(\mathrm{F}_{\mathrm{S}}=\mathrm{F}_{\mathrm{S}, \mathrm{E}} \mathrm{kg}\) solvent \(/ \mathrm{h}\), which is an effective solvent rate. Partial miscibility will be ignored, and its effect will be included in \(\mathrm{F}_{\mathrm{S}, \mathrm{E}}\) and in the effective equilibrium constant \(\mathrm{m}_{\mathrm{E}}, \mathrm{Y}=\mathrm{m}_{\mathrm{E}} \mathrm{X}\) where \(Y=\mathrm{kg}\) oil/ \(\mathrm{kg}\) solvent and \(\mathrm{X}=\mathrm{kg}\) oil/ \(\mathrm{kg}\) meal. From the results of Example 14-2, find the values of \(\mathrm{F}_{S, \text { avg }}\) and \(\mathrm{m}_{E}\) that satisfy both the Kremser equation (written in terms of ratios \(\mathrm{Y}\) and \(\mathrm{X}\) ) and the external oil mass balance. Note that \(\mathrm{F}_{\mathrm{S}, \text { in }}=662>\mathrm{F}_{\mathrm{S}, \mathrm{E}}\). Assume extra solvent is used to saturate the meal and \(\mathrm{F}_{\mathrm{S}, \mathrm{E}}\) is solvent available to do the separation. Do Problem 14.A10 immediately after solving 14.D11.

Example 14-2

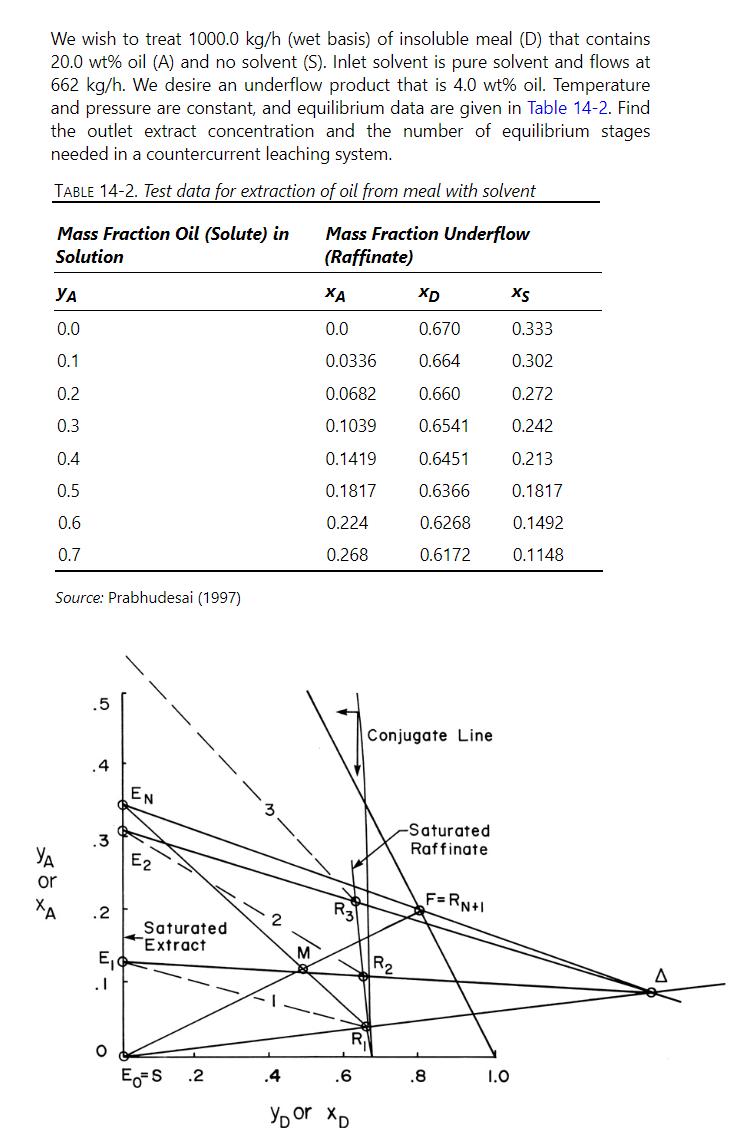
Data From Problem 14.D10

Use of slurry adsorbents has received some industrial attention because it allows for countercurrent movement of the solid and fluid phases. Your manager wants you to design a slurry adsorbent system for removing methane from a hydrogen gas stream. The actual separation process is a complex combination of adsorption and absorption, but total equilibrium can be represented by a simple equation. At \(5.0^{\circ} \mathrm{C}\), equilibrium can be represented as

\section*{Weight fraction \(\mathrm{CH}_{4}\) in gas \(=1.2 \times\) (weight fraction \(\mathrm{CH}_{4}\) in slurry)}

At \(5.0^{\circ} \mathrm{C}\), no hydrogen could be detected in the slurry, and heat of sorption was negligible. We wish to separate a gas feed at \(5.0^{\circ} \mathrm{C}\) that contains 100.0 \(\mathrm{lb} / \mathrm{h}\) of hydrogen and \(30.0 \mathrm{lb} / \mathrm{h}\) of methane. An outlet gas concentration of \(5.0 \mathrm{wt} \%\) methane is desired. Entering slurry contains no methane and flows at a rate of \(120.0 \mathrm{lb} / \mathrm{h}\). Find the number of equilibrium stages required for this separation and the mass fraction of methane leaving in the slurry.

We wish to treat 1000.0 kg/h (wet basis) of insoluble meal (D) that contains 20.0 wt% oil (A) and no solvent (S). Inlet solvent is pure solvent and flows at 662 kg/h. We desire an underflow product that is 4.0 wt% oil. Temperature and pressure are constant, and equilibrium data are given in Table 14-2. Find the outlet extract concentration and the number of equilibrium stages needed in a countercurrent leaching system. TABLE 14-2. Test data for extraction of oil from meal with solvent Mass Fraction Oil (Solute) in Solution Mass Fraction Underflow (Raffinate) XD XS 0.0 0.0 0.670 0.333 0.1 0.0336 0.664 0.302 0.2 0.0682 0.660 0.272 0.3 0.1039 0.6541 0.242 0.4 0.1419 0.6451 0.213 0.5 0.1817 0.6366 0.1817 0.6 0.224 0.6268 0.1492 0.7 0.268 0.6172 0.1148 Source: Prabhudesai (1997) .5 .4 EN 3 XOX or .3 .2 E2 Saturated Extract .1 Conjugate Line R3 -Saturated Raffinate F=RN+I 2 M R R E=S .2 .4 .6 .8 1.0 YD or XD