Maximum likelihood estimation of the two-way random effects model.} (a) Using the concentrated likelihood function in (3.32),
Question:
Maximum likelihood estimation of the two-way random effects model.}
(a) Using the concentrated likelihood function in (3.32), solve \(\partial L_{C} / \partial \beta=0\), given \(\phi_{2}^{2}\) and \(\phi_{3}^{2}\), and verify (3.33).
(b) Solve \(\partial L_{C} / \partial \phi_{2}^{2}=0\), given \(\phi_{3}^{2}\) and \(\beta\), and verify (3.34).
(c) Solve \(\partial L_{C} / \partial \phi_{3}^{2}=0\), given \(\phi_{2}^{2}\) and \(\beta\), and show that the solution \(\phi_{3}^{2}\) satisfies
\[\bar{a} \phi_{3}^{4}+\bar{b} \phi_{3}^{2}+\bar{c}=0\]
where
\[\begin{aligned}& \bar{a}=-[T(N-1)+1]\left(1-\phi_{2}^{2}ight)\left(d^{\prime} Q_{3} dight) \\& \bar{b}=\left(1-\phi_{2}^{2}ight)(T-1) d^{\prime}\left[Q_{1}+\phi_{2}^{2} Q_{2}ight] d-\phi_{2}^{2} T(N-1) d^{\prime} Q_{3} d\end{aligned}\]
and
\[\bar{c}=T \phi_{2}^{2} d^{\prime}\left(Q_{1}+\phi_{2}^{2} Q_{2}ight) d\]
Note that this is analogous to (3.35), with \(\phi_{2}^{2}\) replacing \(\phi_{3}^{2}, N\) replacing \(T\), and \(Q_{2}\) replacing \(Q_{3}\) and vice versa, wherever they occur.
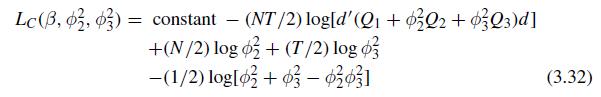
![]()
Step by Step Answer:






