Determine the displacement field for the beam problem in Exercise 8.2. To determine the rigid body motion terms, choose fixity conditions:

Note that with our approximate Saint-Veran solution, we cannot ensure pointwise conditions all along the built-in end. Finally, for the special case with N = 0, compare the elasticity displacement field with the corresponding results from mechanics of materials theory (see Appendix D).

Data from appendix D

Beginning undergraduate studies of the mechanics of deformable solids are normally taught in a course called mechanics of materials or strength of materials. Based on very restrictive assumptions, this study develops stress, strain, and displacement field solutions for a very limited class of elastic solids with simple geometry. Strength of materials theory commonly makes use of assumptions on the geometry of the deformation (e.g., plane sections remain plane) and thus assumes the distribution of displacements and strains. Further simplification is also sometimes made on the stress field. Because of the level of approximation, strength of materials is often referred to as the elementary theory when compared to the more exact elasticity model. Nevertheless, decades of application have shown that mechanics of materials provides reasonable estimates for many practical stress analysis problems.

Furthermore, strength of materials solutions have provided guidance for the development of particular elasticity solutions.  We now pursue a brief review of the basic strength of materials solutions of extension, torsion, and  bending/shear of elastic rods and beams, as shown in Fig. D.1. Rod and beam structures are normally  defined as prismatic solids with a length dimension much larger than the other two dimensions located within the cross-section. General loadings to such structures commonly include axial force P, shear force V, torque T, and bending moment M. Mechanics of materials theory develops an approximate solution for each of these four loading types.  Commonly these solutions will be restricted to cases with particular cross-sectional shapes that are  related to section properties of A = area, J = polar moment of inertia, and I = rectangular moment of :

 inertia. Because these solutions are useful to compare with related elasticity models, we now briefly review their development. In addition to these problems, we review curved beams and cylindrical pressure vessels.

Data from exercise 8.2

Show that the Airy function:

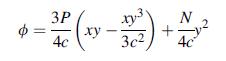
solves the following cantilever beam problem, as shown in the following figure. As usual for such problems, boundary conditions at the ends (x = 0 and L) should be formulated only in terms of the resultant force system, while at y = ± c the exact pointwise specification should be used. For the case with N = 0, compare the elasticity stress field with the corresponding results from strength of materials theory.

Transcribed Image Text:

u(L, 0) = v(L,0) = av(L,0) = 0