Consider the GLMM in (9.11) with a logit link. Show that (a) (Eleft(y_{i t} mid mathbf{x}_{i t},
Question:
Consider the GLMM in (9.11) with a logit link. Show that
(a) \(E\left(y_{i t} \mid \mathbf{x}_{i t}, \mathbf{z}_{i t}\right) \approx \Phi\left(\frac{\mathbf{x}_{i t}^{\top} \beta}{\sqrt{c^{2}+\mathbf{z}_{i t}^{\top} \Sigma_{b} \mathbf{z}_{i t}}}\right)\), where \(c=\frac{15 \pi}{16 \sqrt{3}}\) and \(\Phi(\cdot)\) denotes the cumulative distribution function of the standard normal with mean 0 and variance 1 (see Johnson et al. (1994)).
(b) \(\Phi\left(\frac{\mathbf{x}_{i t}^{\top} \beta}{\sqrt{c^{2}+\mathbf{z}_{i t}^{\top} \Sigma_{b} \mathbf{z}_{i t}}}\right) \approx \operatorname{logit}^{-1}\left(\left(1+c^{-2} \mathbf{z}_{i t}^{\top} \Sigma_{b} \mathbf{z}_{i t}\right)^{-\frac{1}{2}} \mathbf{x}_{i t}^{\top} \beta\right)\).
(c) if \(\mathbf{z}_{i t}=\mathbf{z}_{t}\), i.e., \(\mathbf{z}_{i t}\) is independent of individual characteristics, then \(\boldsymbol{\beta}_{M} \approx\) \(\left(1+c^{-2} \mathbf{z}_{t}^{\top} \Sigma_{b} \mathbf{z}_{t}\right)^{-\frac{1}{2}} \boldsymbol{\beta}\), where \(\boldsymbol{\beta}_{M}\) is the parameter of the corresponding marginal model.
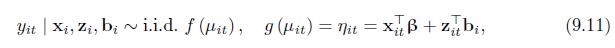
Step by Step Answer:

Applied Categorical And Count Data Analysis
ISBN: 9780367568276
2nd Edition
Authors: Wan Tang, Hua He, Xin M. Tu





