Solve the following LP problem by the dual simplex method

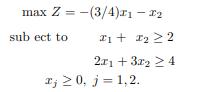
a) Exhibit the optimal primal solution and the corresponding optimal primal basis. Exhibit the dual optimal solution.

b) The primal solution is degenerate. To study the implications of degeneracy, graph the primal output and input spaces. Notice that in the primal output space three constraints intersect at the optimal extreme point. Notice that in the primal input space, the RHS vector is coincident with one of the basic vectors. Graph the dual problem and verify that the ob ective function is parallel to one of the constraints generating, therefore, two optimal solutions.

c) Starting from the optimal tableau obtained in a), and using the dual simplex algorithm, calculate the second dual optimal solution.

d) Exhibit the two extreme-point dual optimal solutions.

e) Obtain an optimal dual solution that contains three positive components.
Explain your work.

max Z (3/4)21-22 sub ect to = 21+2 2 2x1 +32 4 x; 0, j = 1,2.