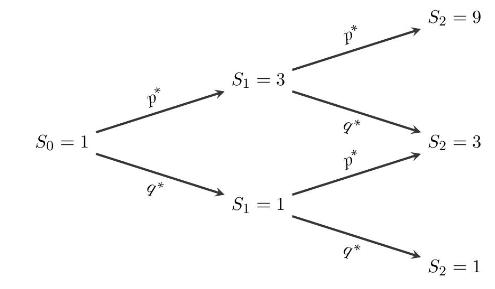
CRR model with dividends (1). Consider a two-step binomial model for a stock paying a dividend at the rate \(\alpha \in(0,1)\) at times \(k=1\) and \(k=2\), and the following recombining tree represents the ex-dividend \({ }^{*}\) prices \(S_{k}\) at times \(k=1,2\), starting from \(S_{0}=\$ 1\).

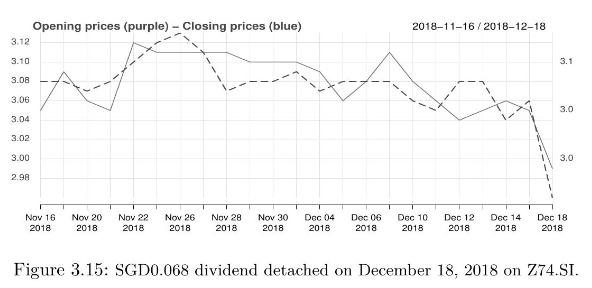
The difference between the closing price on December 17 (\$3.06) and the opening price on December \(18(\$ 2.99)\) is \(\$ 3.06-\$ 2.99=\$ 0.07\). The adjusted price on December 17 (\$2.992) is the closing price (\$3.06) minus the dividend (\$0.068).

The dividend rate \(\alpha\) is given by \(\alpha=0.068 / 3.06=2.22 \%\).
We consider a riskless asset \(A_{k}=A_{0}(1+r)^{k}, k=0,1,2\) with interest rate \(r=100 \%\) and \(A_{0}=1\), and two portfolio allocations \(\left(\xi_{1}, \eta_{1}ight)\) at time \(k=0\) and \(\left(\xi_{2}, \eta_{2}ight)\) at time \(k=1\), with the values \[
\begin{equation*}
V_{1}=\xi_{2} S_{1}+\eta_{2} A_{1} \tag{3.50}
\end{equation*}
\]
and \[
\begin{equation*}
V_{0}=\xi_{1} S_{0}+\eta_{1} A_{0} \tag{3.51}
\end{equation*}
\]
We make the following three assumptions:
[A] All dividends are reinvested.
[B] The portfolio strategies are self-financing.
[C] The portfolio value \(V_{2}\) at time \(k=2\) hedges the European call option with payoff \(C=\left(S_{T}-Kight)^{+}\), strike price \(K=8\), and maturity \(T=2\).

a) Using (3.50) and [A], express \(V_{2}\) in terms of \(\xi_{2}, \eta_{2}, S_{2}, A_{2}\) and \(\alpha\).

b) Using (3.51) and [A]-[B], express \(V_{1}\) in terms of \(\xi_{1}, \eta_{1}, S_{1}, A_{1}\) and \(\alpha\).

c) Using Assumption [C] and the result of Question (a), compute the portfolio allocation \(\left(\xi_{2}, \eta_{2}ight)\) in cases \(S_{1}=1\) and \(S_{1}=3\).

d) Using (3.50) and the portfolio allocation \(\left(\xi_{2}, \eta_{2}ight)\) obtained in Question (c), compute the portfolio value \(V_{1}\) in cases \(S_{1}=1\) and \(S_{1}=3\).

e) From the results of Questions

(b) and (d), compute the initial portfolio allocation \(\left(\xi_{1}, \eta_{1}ight)\).

f) Compute the initial portfolio value \(V_{0}\) from the result of Question (e).
g) Knowing that the dividend rate is \(\alpha=25 \%\), draw the tree of asset prices \(\left(\bar{S}_{k}ight)_{k=1,2}\) before (i.e. without) dividend payments.

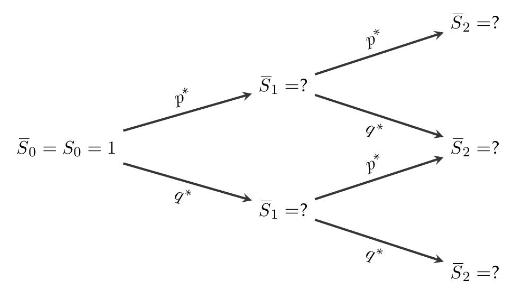
h) Compute the risk-neutral probabilities \(p^{*}\) and \(q^{*}\) under which the conditional expected return of \(\left(\bar{S}_{k}ight)_{k=0,1,2}\) is the risk-free interest rate \(r=100 \%\).
i) \(\checkmark\) Check that the portfolio value \(V_{1}\) found in Question

(d) satisfies \[
V_{1}=\frac{1}{1+r} \mathbb{E}^{*}\left[\left(S_{2}-Kight)^{+} \mid S_{1}ight]
\]
j) \(\checkmark\) Check that the portfolio value \(V_{0}\) found in Question

(f) satisfies \[
V_{0}=\frac{1}{(1+r)^{2}} \mathbb{E}^{*}\left[\left(S_{2}-Kight)^{+}ight] \quad \text { and } \quad V_{0}=\frac{1}{1+r} \mathbb{E}^{*}\left[V_{1}ight]
\]

Transcribed Image Text:

So = 1 p* q* S = 3 S = 1 P* P 9* S = 9 S = 3 S = 1