Let (left(N_{t} ight)_{t in[0, T]}) be a standard Poisson process started at (N_{0}=0), with intensity (lambda>0) under

Let \(\left(N_{t}\right)_{t \in[0, T]}\) be a standard Poisson process started at \(N_{0}=0\), with intensity \(\lambda>0\) under the probability measure \(\mathbb{P}_{\lambda}\), and consider the compound Poisson process \(\left(Y_{t}\right)_{t \in[0, T]}\) with i.i.d. jump sizes \(\left(Z_{k}\right)_{k \geqslant 1}\) of distribution \(u(d x)\).

a) Under the probability measure \(\mathbb{P}_{\lambda}\), the process \(t \mapsto Y_{t}-\lambda t(t+\mathbb{E}[Z])\) is a:

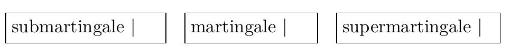
b) Consider the process \(\left(S_{t}\right)_{t \in[0, T]}\) given by

\[d S_{t}=\mu S_{t} d t+\sigma S_{t^{-}} d Y_{t}\]

Find \(\tilde{\lambda}\) such that the discounted process \(\left(\widetilde{S}_{t}\right)_{t \in[0, T]}:=\left(e^{-r t} S_{t}\right)_{t \in[0, T]}\) is a martingale under the probability measure \(\mathbb{P}_{\tilde{\lambda}}\) defined by the Radon-Nikodym density

\[\frac{\mathrm{d} \mathbb{P}_{\tilde{\lambda}}}{\mathrm{d} \mathbb{P}_{\lambda}}:=\mathrm{e}^{-(\tilde{\lambda}-\lambda) T}\left(\frac{\tilde{\lambda}}{\lambda}\right)^{N_{T}}\]

with respect to \(\mathbb{P}_{\lambda}\).

c) Price the forward contract with payoff \(S_{T}-\kappa\).

Transcribed Image Text:

submartingale | martingale | supermartingale |