Let G = (V, E) be a directed graph with weight function w : E ⇾ R, and let n = |V|. We define the mean weight of a cycle c = ⟨e₁, e₂, . . . , e_k⟩ of edges in E to be

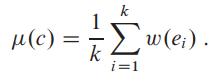
Let μ^* = min_c μ(c), where c ranges over all directed cycles in G. We call a cycle c for which μ (c) = μ^* a minimum mean-weight cycle. This problem investigates an efficient algorithm for computing μ^*.

Assume without loss of generality that every vertex v ∈ V is reachable from a source vertex s ∈ V. Let δ (s, v) be the weight of a shortest path from s to v, and letδ_k (s, v) be the weight of a shortest path from s to v consisting of exactly k edges. If there is no path from s to v with exactly k edges, then δ_k (s, v) = ∞.

a. Show that if μ^* = 0, then G contains no negative-weight cycles and δ (s, v) = min_{0 ≤ k ≤ n - 1} δ _k (s, v) for all vertices v ∈ V.

b. Show that if μ^*= 0, then

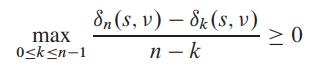
for all vertices v ∈ V.

c. Let c be a 0-weight cycle, and let u and v be any two vertices on c. Suppose that μ^* = 0 and that the weight of the simple path from u to v along the cycle is x. Prove that δ (s, ?) = δ (s, u) + x. The weight of the simple path from u to v along the cycle is −x.

d. Show that if μ^* = 0, then on each minimum mean-weight cycle there exists a vertex v such that

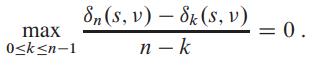
Show how to extend a shortest path to any vertex on a minimum mean weight cycle along the cycle to make a shortest path to the next vertex on the cycle.

e. Show that if μ^* = 0, then

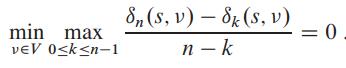
f. Show that if we add a constant t to the weight of each edge of G, then μ^* increases by t. Use this fact to show that

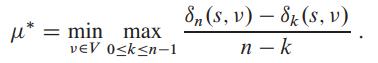
g. Give an O(VE)-time algorithm to compute μ^*.

max O