The decomposition of the sums of squares into a contribution due to error and a contribution due to regression underlies the least squares analysis. Consider the identity

\[y_{i}-\bar{y}-\left(\widehat{y}_{i}-\bar{y}\right)=\left(y_{i}-\widehat{y}_{i}\right)\]

Note that

\[\begin{aligned} & \widehat{y}_{i}=a+b x_{i}=\bar{y}-b \bar{x}+b x_{i}=\bar{y}+b\left(x_{i}-\bar{x}\right) \text { so } \\ & \widehat{y}_{i}-\bar{y}=b\left(x_{i}-\bar{x}\right) \end{aligned}\]

Using this last expression, then the definition of \(b\) and again the last expression, we see that \[\begin{aligned} & \sum\left(y_{i}-\bar{y}\right)\left(\widehat{y}_{i}-\bar{y}\right)=b \sum\left(y_{i}-\bar{y}\right)\left(x_{i}-\bar{x}\right) \\ & \quad=b^{2} \sum\left(x_{i}-\bar{x}\right)^{2}=\sum\left(\widehat{y}_{i}-\bar{y}\right)^{2} \end{aligned}\]
and the sum of squares about the mean can be decomposed as \[\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}\]
total sum of squares \[\begin{aligned} & =\quad \sum_{i=1}^{n}\left(y_{i}-\widehat{y}_{i}\right)^{2}+\sum_{i=1}^{n}\left(\widehat{y}_{i}-\bar{y}\right)^{2} \\ & \text { error sum of squares } \quad \text { regression sum of squares } \end{aligned}\]
Generally, we find the straight-line fit acceptable if the ratio \(r^{2}=\frac{\text { regression sum of squares }}{\text { total sum of squares }}=1-\frac{\sum_{i=1}^{n}\left(y_{i}-\widehat{y}_{i}\right)^{2}}{\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}\)
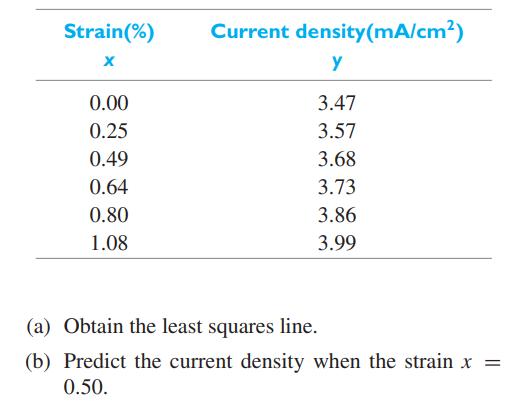
is near 1 . Calculate the decomposition of the sum of squares and calculate \(r^{2}\) using the observations in Exercise 11.9.

Data From Exercise 11.9

Transcribed Image Text:

11.9 Scientists searching for higher performance flexible structures created a diode with organic and inorganic layers. It has excellent mechanical bending proper- ties. Applying a bending strain to the diode actually leads to higher current density(mA/cm). Metal curva- ture molds, each having a different radius, were used to apply strain(%). For one demonstration of the phe- nomena, the data are