Let (left{f_{n}(x)ight}_{n=1}^{infty}) be a sequence of real functions defined by (f_{n}(x)=(1+) (left.n^{-1}ight) delta{x ;(0,1)}) for all (n
Question:
Let \(\left\{f_{n}(x)ight\}_{n=1}^{\infty}\) be a sequence of real functions defined by \(f_{n}(x)=(1+\) \(\left.n^{-1}ight) \delta\{x ;(0,1)\}\) for all \(n \in \mathbb{N}\).
a. Prove that
\[\lim _{n ightarrow \infty} f_{n}(x)=\delta\{x ;(0,1)\}\]
for all \(x \in \mathbb{R}\), and hence conclude that
\[\int_{-\infty}^{\infty} \lim _{n ightarrow \infty} f_{n}(x) d x=1\]
b. Compute
\[\lim _{n ightarrow \infty} \int_{-\infty}^{\infty} f_{n}(x) d x\]
Does this match the result you found above?
c. State whether Theorem 1.11 applies to this case, and use it to explain the results you found above.
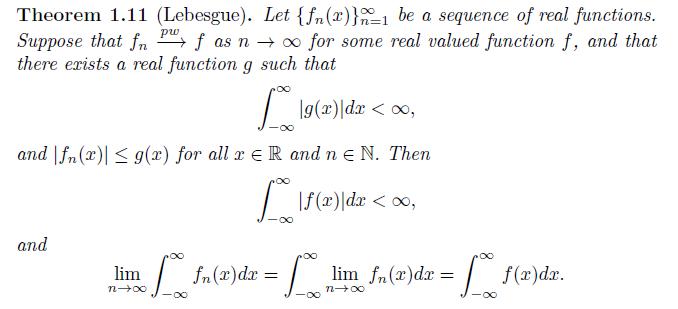
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





