Consider the fractals introduced in Problems 1.4 and 1.5: the Koch snowflake and the Sierpiski triangle. Give

Consider the fractals introduced in Problems 1.4 and 1.5: the Koch snowflake and the Sierpiński triangle. Give a heuristic argument that the Hausdorff dimension of the Sierpiński triangle is \(\log 3 / \log 2\). What is the dimension of the Koch snowflake?

Data from problem 1.4

 Let \(K_{0} \subset \mathbb{R}^{2}\) be a line of length 1 . We get \(K_{1}\) by replacing the middle third of \(K_{0}\) by the sides of an equilateral triangle. By iterating this procedure we get the curves \(K_{0}, K_{1}, K_{2}, \ldots\) (see Fig. 1.5) which defines in the limit Koch's snowflake \(K_{\infty}\). Find the length of \(K_{n}\) and \(K_{\infty}\).

Figure 1.5

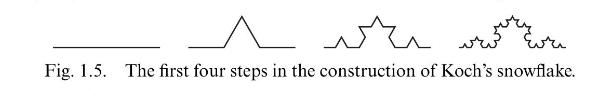
Data from problem 1.5

Let \(S_{0} \subset \mathbb{R}^{2}\) be a solid equilateral triangle. We get \(S_{1}\) by removing the middle triangle whose vertices are the midpoints of the sides of \(S_{1}\). By repeating this procedure with the four triangles which make up \(S_{1}\) etc. we get \(S_{0}, S_{2}, S_{2}, \ldots\) (see Fig. 1.6). The Sierpiński triangle is \(S_{\infty}:=\bigcap_{n=0}^{\infty} S_{n}\). Find the area of \(S_{n}\) and \(S\) if the side-length of \(S_{0}\) is \(s=1\).

Figure 1.6

Transcribed Image Text:

Fig. 1.5. The first four steps in the construction of Koch's snowflake.