Define (phi: mathbb{R} ightarrow mathbb{R}) by (phi(x):=(1-cos x) mathbb{1}_{[0,2 pi)}(x)), let (u(x):=1, v(x):=phi^{prime}(x)) and (w(x):=int_{(-infty, x)} phi(t)
Question:
Define \(\phi: \mathbb{R} ightarrow \mathbb{R}\) by \(\phi(x):=(1-\cos x) \mathbb{1}_{[0,2 \pi)}(x)\), let \(u(x):=1, v(x):=\phi^{\prime}(x)\) and \(w(x):=\int_{(-\infty, x)} \phi(t) d t\). Then
(i) \(u \star v(x)=0\) for all \(x \in \mathbb{R}\);
(ii) \(v \star w(x)=\phi \star \phi(x)>0\) for all \(x \in(0,4 \pi)\);
(iii) \((u \star v) \star w \equiv 0 eq u \star(v \star w)\).
Does this contradict the associativity of the convolution which is implicit in Theorem 15.6 ?
Data from problem 15.6
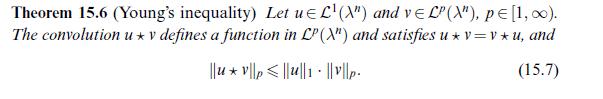


Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





