Find a sequence of integrable functions ( u n ) n N ( u n ) n N with u n ( x

Find a sequence of integrable functions ${\left(u_n\right)}_{n\in N}$ with $u_n\left(x\right)\to u\left(x\right)$ for all $x$ and an integrable function $u$ but such that ${lim}_{n\to \infty }\int u_{n}d\mu \ne \int ud\mu$. Does this contradict Lebesgue's dominated convergence theorem (Theorem 12.2 )?

Data from theorem 12.2

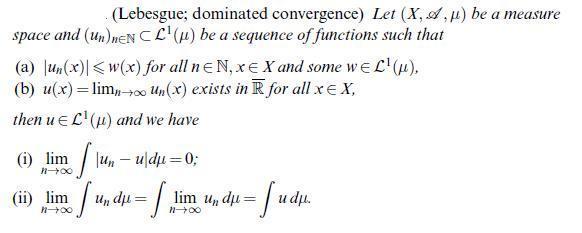
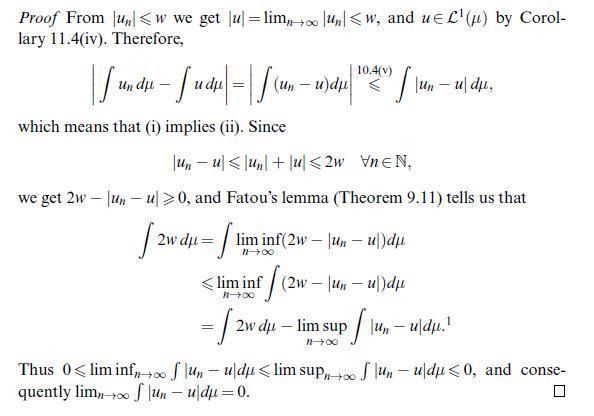
(Lebesgue; dominated convergence) Let (X, A, u) be a measure space and (un)nEN CL () be a sequence of functions such that (a) un(x)