In Example 12.15 we introduced Euler's gamma function: [Gamma(t)=int_{(0, infty)} x^{t-1} e^{-x} lambda^{1}(d x)] Show that (Gammaleft(frac{1}{2}ight)=sqrt{pi}).
Question:
In Example 12.15 we introduced Euler's gamma function:
\[\Gamma(t)=\int_{(0, \infty)} x^{t-1} e^{-x} \lambda^{1}(d x)\]
Show that \(\Gamma\left(\frac{1}{2}ight)=\sqrt{\pi}\).
Data from example 12.15
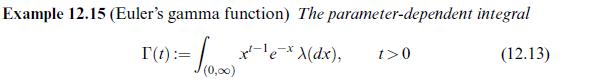



Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





