Non-measurable sets (2). Consider on (X=mathbb{R}) the (sigma)-algebra (mathscr{A}:=left{A subset mathbb{R}: Aight.) or (A^{c}) is countable }
Question:
Non-measurable sets (2). Consider on \(X=\mathbb{R}\) the \(\sigma\)-algebra \(\mathscr{A}:=\left\{A \subset \mathbb{R}: Aight.\) or \(A^{c}\) is countable \} from Example 3.3 (v) and the measure \(\gamma(A)\) from Example 4.5 (ii), which is 0 or 1 according to \(A\) or \(A^{c}\) being countable. Denote by \(\gamma^{*}\) and \(\mathscr{A}^{*}\) the outer measure and \(\sigma\)-algebra which appear in the proof of Theorem 6.1 .
(i) Find \(\gamma^{*}\) if we use \(\mathcal{S}=\mathscr{A}\) in Theorem 6.1 .
(ii) Show that no set \(B \subset \mathbb{R}\), such that both \(B\) and \(B^{c}\) are uncountable, is in \(\mathscr{A}\) or in \(\mathscr{A}^{*}\).
Data from theorem 6.1
![(Carathodory) Let S P(X) be a semi-ring and u: S [0, ] a pre-measure, i.e. a set function with (i) (0) = 0;](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/3/6/88565a9f415b01bd1705636885415.jpg)
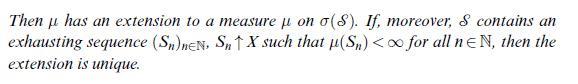
Data from example 4.5

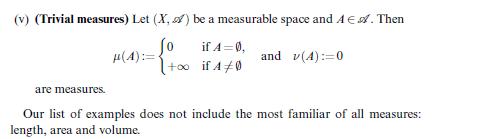
Data from example 3.3


Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





