This exercise shows the following theorem. Theorem (Frchet-von Neumann-Jordan). An inner product (langlecdot, cdotangle) on the (mathbb{R})-vector
Question:
This exercise shows the following theorem.
Theorem (Fréchet-von Neumann-Jordan). An inner product \(\langle\cdot, \cdotangle\) on the \(\mathbb{R}\)-vector space \(V\) derives from a norm if, and only if, the parallelogram identity (26.3) holds.
(i) Necessity: prove Lemma 26.6 .
Assume from now on that \(\|\cdot\|\) is a norm satisfying (26.3) and set
\[(v, w):=\frac{1}{4}\left(\|v+w\|^{2}-\|v-w\|^{2}ight)\]
(ii) Show that \((v, w)\) satisfies the properties \(\left(\mathrm{SP}_{1}ight)\) and \(\left(\mathrm{SP}_{2}ight)\) of Definition 26.2 .
(iii) Prove that \((u+v, w)=(u, w)+(v, w)\).
(iv) Use (iii) to prove that \((q v, w)=q(v, w)\) for all dyadic numbers \(q=n 2^{-k}, n \in \mathbb{Z}\), \(k \in \mathbb{N}_{0}\), and conclude that \(\left(\mathrm{SP}_{3}ight)\) holds for dyadic \(\alpha, \beta\).
(v) Prove that the maps \(t \mapsto\|t v+w\|\) and \(t \mapsto\|t v-w\|(t \in \mathbb{R}, v, w \in V)\) are continuous and conclude that \(t \mapsto(t v, w)\) is continuous. Use this and (iv) to show that \(\left(\mathrm{SP}_{3}ight)\) holds for all \(\alpha, \beta \in \mathbb{R}\).
Equation 26.3
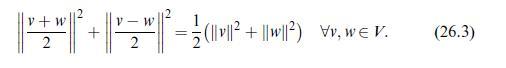
Data from lemma 26.6

Step by Step Answer:






