Use Theorem 21.18 for a new proof of Lvy's continuity theorem (Problem 21.3 ). (i) Show (as

Use Theorem 21.18 for a new proof of Lévy's continuity theorem (Problem 21.3 ).

(i) Show (as in Problem 21.3 ) that \(\lim _{i ightarrow \infty} \int u d \mu_{i}\) exists for all \(u \in C_{c}\left(\mathbb{R}^{n}ight)\). Since \(u \in C_{c}\left(\mathbb{R}^{n}ight)\) implies \(|u| \in C_{c}\left(\mathbb{R}^{n}ight)\), the sequence is vaguely bounded and there is a measure \(\mu\) and a vaguely convergent subsequence \(\mu_{n(i)} ightarrow \mu\).

(ii) Part (i) can be applied to every subsequence of \(\left(\mu_{i}ight)_{i}\) and it follows that every subsequence contains a vaguely convergent sub-subsequence, all of which have the same limit \(\mu\). Therefore, \(\mu_{i} ightarrow \mu\) vaguely.

(iii) Use Lévy's truncation inequality (Problem 19.6 ) to show the tightness of the measures \(\left(\mu_{i}ight)_{i}\); Theorem 21.17 proves that \(\mu_{i} ightarrow \mu\) weakly.

Data from theorem 21.18

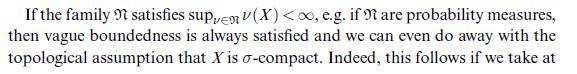
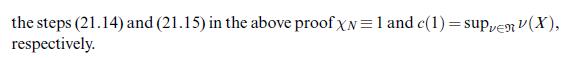
Data from problem 21.3

Lévy's continuity theorem. The steps below sketch a proof of the following theorem.
Theorem (P. Lévy; continuity theorem). Let \(\left(\mu_{i}ight)_{i \in \mathbb{N}}\) be a sequence of finite measures on \(\left(\mathbb{R}^{n}, \mathscr{B}\left(\mathbb{R}^{n}ight)ight)\). If the sequence of Fourier transforms \(\left(\widehat{\mu}_{n}ight)_{n \in \mathbb{N}}\) converges pointwise to a function \(\phi\) which is continuous at \(\xi=0\), then there is a finite measure \(\mu\) such that \(\mu_{i} ightarrow \mu\) weakly. In particular, \(\widehat{\mu}=\phi\) and the convergence of the functions \(\widehat{\mu}_{i}\) is locally uniform.

Data from problem 19.6

Let \(\mu\) be a finite measure on \(\left(\mathbb{R}^{n}, \mathscr{B}\left(\mathbb{R}^{n}ight)ight)\). Prove P. Lévy's truncation inequality:
\[
\mu\left(\mathbb{R}^{n} \backslash[-2 R, 2 R]^{n}ight) \leqslant 2\left(\frac{R}{2}ight)^{n} \int_{[-1 / R, 1 / R]^{n}}\left(\mu\left(\mathbb{R}^{n}ight)-\operatorname{Re} \breve{\mu}(\xi)ight) d \xi
\]
[ show that the right-hand side equals
\[
2 \int\left(1-\prod_{1}^{n} \frac{\sin \left(x_{n} / Right)}{x_{n} / R}ight) \mu(d x)
\]
shrink the integration domain to \(\mathbb{R}^{n} \backslash[-2 R, 2 R]^{n}\) and observe that \(0 \leqslant \frac{1}{2} \sin 2 \leqslant \frac{1}{2}\) and \(x^{-1} \sin x

Transcribed Image Text:

Theorem 21.18 Let (X, d) be a locally compact and o-compact metric space such that (C(X), ||- ||) is separable. If NCM(X) is vaguely bounded, i.e. VE udv=c(u)