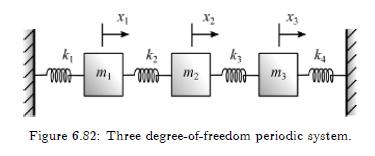
(a) For the three degree-of-freedom system shown in Figure 6.82, derive the equations of motion and solve for the frequencies and modes of vibration for the arbitrary stiffnesses \(k_{1}, k_{2}, k_{3}, k_{4}\) and masses \(m_{1}, m_{2}, m_{3}\). Then simplify these results for the case where all the stiffnesses have the value \(k=1 \mathrm{~N} / \mathrm{m}\) and all the masses have the value \(m=1 \mathrm{~kg}\). Plot the modes and responses for \(x_{1}(0)=0.5 \mathrm{~cm}\) and assume that all other initial conditions are equal to zero.

(b) For the previous system, suppose that \(k_{1}=k_{3}=\) \(k_{4}=k=1 \mathrm{~N} / \mathrm{m}, m_{1}=m_{2}=m_{3}=m=1 \mathrm{~kg}\), and \(k_{2}=(1+\epsilon) k=(1+0.05) k\), where \(\epsilon\) signifies a stiffness imperfection. Solve for the frequencies and modes of vibration and plot the modes and responses for \(x_{1}(0)=0.5 \mathrm{~cm}\) and all other initial conditions equal zero.

Compare the results with and without imperfections.Discuss.

Transcribed Image Text:

ka mm m ww m mw m3 mm Figure 6.82: Three degree-of-freedom periodic system.