The system in Figure 5.45 oscillates about the equilibrium position denoted by the horizontal lines. The coil
Question:
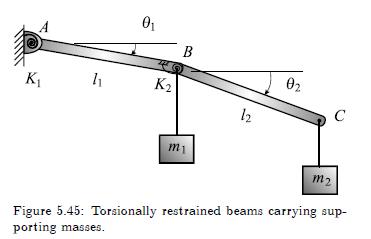
The system in Figure 5.45 oscillates about the equilibrium position denoted by the horizontal lines. The coil torsional springs are each undeformed when \(\theta_{1}=\theta_{2}=0\). If the link masses are neglected, derive the equations of motion to be
\[ \begin{aligned} \left(m_{1}+m_{2}\right) l_{1}^{2} \ddot{\theta}_{1}+m_{2} l_{1} l_{2} \ddot{\theta}_{2} \cos \left(\theta_{2}-\theta_{1}\right) \\ -m_{2} l_{1} l_{2} \dot{\theta}_{2} \dot{\theta}_{2} \sin \left(\theta_{2}-\theta_{1}\right)+\left(K_{1}+K_{2}\right) \theta_{1} \\ -K_{2} \theta_{2}-\left(m_{1}+m_{2}\right) g l_{1} \cos \theta_{1}=0 \\ m_{2} l_{2}^{2} \ddot{\theta}_{2}+m_{2} l_{1} l_{2} \ddot{\theta}_{1} \cos \left(\theta_{2}-\theta_{1}\right) \\ +m_{2} l_{1} l_{2} \dot{\theta}_{1}^{2} \sin \left(\theta_{2}-\theta_{1}\right)+K_{2}\left(\theta_{2}-\theta_{1}\right) \\ -m_{2} g l_{2} \cos \theta_{2}=0 \end{aligned} \]
Step by Step Answer:

Mechanical Vibration Analysis, Uncertainties, And Control
ISBN: 9781498753012
4th Edition
Authors: Haym Benaroya, Mark L Nagurka, Seon Mi Han





