By using the matrix techniques discussed in the next-to-the-last paragraph of Box 12.2, deduce that the general
Question:
By using the matrix techniques discussed in the next-to-the-last paragraph of Box 12.2, deduce that the general solution to the algebraic wave equation (12.6) is the sum of a longitudinal mode with the properties deduced in Sec. 12.2.3 and two transverse modes with the properties deduced in Sec. 12.2.4.
Specifically, do the following.
(a) Rewrite the algebraic wave equation in the matrix form Mijξj = 0, obtaining thereby an explicit form for the matrix ||Mij|| in terms of ρ, K, μ, ω and the components of k.
(b) This matrix equation from part (a) has a solution if and only if the determinant of the matrix ||Mij|| vanishes. (Why?) Show that det||Mij|| = 0 is a cubic equation for ω2 in terms of k2, and that one root of this cubic equation is ω = CLk, while the other two roots are ω = CTk with CL and CT given by Eqs. (12.9a) and (12.12a).
(c) Orient Cartesian axes so that k points in the z direction. Then show that, when ω = CLk, the solution to Mijξj = 0 is a longitudinal wave (i.e., a wave with ξ pointing in the z direction, the same direction as k).
(d) Show that, when ω = CTk, there are two linearly independent solutions to Mijξj = 0, one with ξ pointing in the x direction (transverse to k) and the other in the y direction (also transverse to k).
Equations
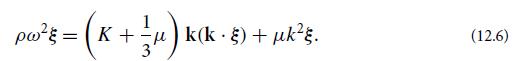
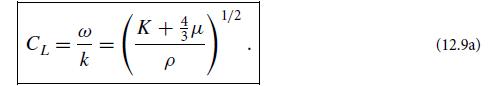






Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





