Consider a collection of identical test particles with rest mass m ≠ 0 that diffuse through a collection of thermalized scattering centers. (The test particles might be molecules of one species, and the scattering centers might be molecules of a much more numerous species.) The scattering centers have a temperature T such that k_BT 2, so if the test particles acquire this temperature, they will have thermal speeds small compared to the speed of light as measured in the mean rest frame of the scattering centers. We study the effects of scattering on the test particles using the following collision-time approximation for the collision terms in the Boltzmann equation, which we write in the mean rest frame of the scattering centers:

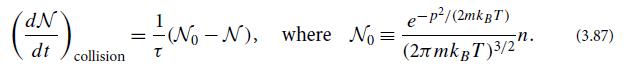
Here the time derivative d/dt is taken moving with a fiducial test particle along its unscattered trajectory, p = |p| is the magnitude of the test particles’ spatial momentum

is the number density of test particles, and τ is a constant to be discussed below.

(a) Show that this collision term preserves test particles in the sense that

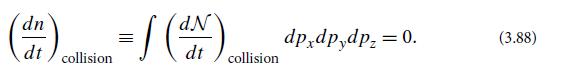
(b) Explain why this collision term corresponds to the following physical picture: Each test particle has a probability 1/τ per unit time of scattering; when it scatters, its direction of motion is randomized and its energy is thermalized at the scattering centers’ temperature.

(c) Suppose that the temperature T is homogeneous (spatially constant), but the test particles are distributed in homogeneously, n = n(x) ≠ const. Let L be the length scale on which their number density n varies. What condition must L, τ, T, and m satisfy for the diffusion approximation to be reasonably accurate? Assume that this condition is satisfied.

(d) Compute, in order of magnitude, the particle flux S = −D∇n produced by the gradient of the number density n, and thereby evaluate the diffusion coefficient D.

(e) Show that the Boltzmann transport equation takes the form (sometimes known as the BKG or Crook model)

(f) Show that to first order in a small diffusion-approximation parameter, the solution of this equation is N = N₀ + N₁, where N₀ is as defined in Eq. (3.87), and

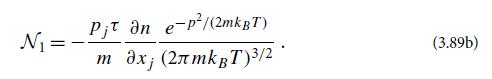
(g) Show that the perturbation N1 gives rise to a particle flux given by Eq. (3.70d), with the diffusion coefficient

How does this compare with your order-of-magnitude estimate in part (d)?

Transcribed Image Text:

(d) dt collision = (No-N)₂ where No = e-p²/(2mk BT) (2лmkµT)³/2¹. (3.87)