Consider cells that reside in a heat and particle bath of a classical, relativistic, perfect gas (Fig.
Question:
Consider cells that reside in a heat and particle bath of a classical, relativistic, perfect gas (Fig. 5.1). Each cell has the same volume V and imaginary walls. Assume that the bath’s temperature T has an arbitrary magnitude relative to the rest mass-energy mc2 of the particles (so the thermalized particles might have relativistic velocities), but require kBT
(a) The number of particles in a chosen cell can be anything from N = 0 to N = ∞. Restrict attention, for the moment, to a situation in which the cell contains a precise number of particles, N. Explain why the multiplicity is M= N! even though the density is so low that the particles’ wave functions do not overlap, and they are behaving classically.
(b) Still holding fixed the number of particles in the cell, show that the number of degrees of freedom W, the number density of states in phase space N states, and the energy EN in the cell are
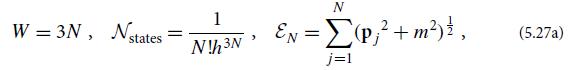
where pj is the momentum of classical particle number j .
(c) Using Eq. (4.8b) to translate from the formal sum over states ∑n to a sum over W = 3N and an integral over phase space, show that the sum over states (5.14) for the grand partition function becomes
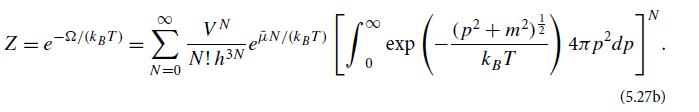
(d) Evaluate the momentum integral in the nonrelativistic limit kBT
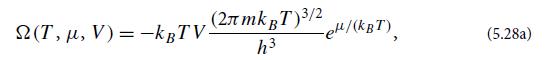
![]()
is the nonrelativistic chemical potential. This is the interaction free limit Vo = a = b = 0 of our grand potential (5.24a) for a van derWaals gas.
(e) Show that in the extreme relativistic limit kBT >> m, Eq. (5.27b) gives
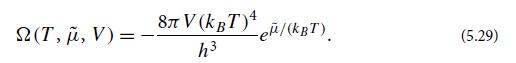
(f) For the extreme relativistic limit use your result (5.29) for the grand potential Ω (V , T , μ̃) to derive the mean number of particles N̅, the pressure P, the entropy S, and the mean energy ε̅ as functions of V , μ̃, and T . Note that for a photon gas, because of the spin degree of freedom, the correct values of N̅, ε̅, and S will be twice as large as what you obtain in this calculation. Show that the energy density is ε̅/V = 3P (a relation valid for any ultra-relativistic gas); and that![]() (which is higher than the 2.7011780 . . . kBT for blackbody radiation, because in the classical regime of η
(which is higher than the 2.7011780 . . . kBT for blackbody radiation, because in the classical regime of η
Figure 5.1
Equation 5.24a.
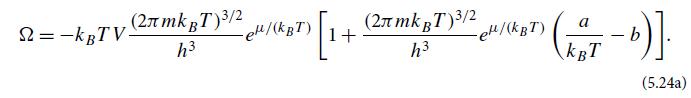
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





