Use the method of moments (Sec. 11.5) to derive the 2-dimensional shape equation (11.63a) for the stress-induced
Question:
Use the method of moments (Sec. 11.5) to derive the 2-dimensional shape equation (11.63a) for the stress-induced deformation of a thin plate, and expression (11.63b) for the 2-dimensional flexural rigidity. Here is a step-by-step guide, in case you want or need it.(a) Show on geometrical grounds that the in-plane strain is related to the vertical displacement by [cf. Eq. (11.40a)]
![]()
(b) Derive an expression for the horizontal components of the stress, Tab, in terms of double derivatives of the displacement function η(x, y) [analog of Txx = −Ezd2η/dx2, Eq. (11.40b), for a stressed rod]. This can be done
(i) By arguing on physical grounds that the vertical component of stress, Tzz, is much smaller than the horizontal components and therefore can be approximated as zero [an approximation to be checked in part (f)];
(ii) By expressing Tzz = 0 in terms of the strain and thence displacement and using Eqs. (11.39) to obtain
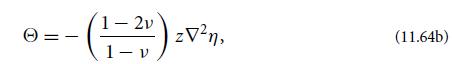
where ∇2 is the horizontal Laplacian; and
(iii) By then writing Tab in terms of Θ and ξa, b and combining with Eqs. (11.64a) and (11.64b) to get the desired equation:
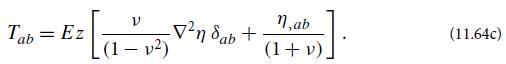
(c) With the aid of Eq. (11.64c), write the horizontal force density in the form
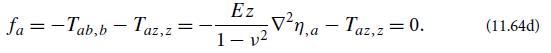
Then, as in the cantilever analysis [Eq. (11.40d)], reduce the dimensionality of this force equation by the method of moments. The zeroth moment (integral over z) vanishes. Why? Therefore, the lowest non vanishing moment is the first (multiply fa by z and integrate). Show that this gives
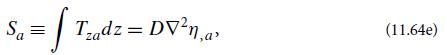
where D is the 2-dimensional flexural rigidity (11.63b). The quantity Sa is the vertical shear force per unit length acting perpendicular to a line in the mirror whose normal is in the direction a; it is the 2-dimensional analog of a stressed rod’s shear force S [Eq. (11.41a)].
(d) For physical insight into Eq. (11.64e), define the bending torque per unit length (bending torque density) as

and show with the aid of Eq. (11.64c) that (11.64e) is the law of torque balance Sa = Mab, b—the 2-dimensional analog of a stressed rod’s S = dM/dx [Eq. (11.42)].
(e) Compute the total vertical shear force acting on a small area of the plate as the line integral of Sa around its boundary, and by applying Gauss’s theorem, deduce that the vertical shear force per unit area is Sa, a. Argue that this must be balanced by the net pressure P applied to the face of the plate, and thereby deduce the law of vertical force balance:
![]()
By combining this equation with the law of torque balance (11.64e), obtain the plate’s bending equation ∇2(∇2η) = P/D[Eq. (11.63a)—the final result we were seeking].
(f) Use this bending equation to verify the approximation made in part (b) that Tzz is small compared to the horizontal stresses. Specifically, show that Tzz ≈ P is O(h/R)2Tab, where h is the plate thickness, and R is the plate radius.
Equations

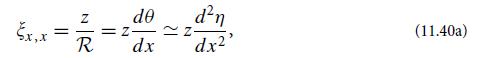

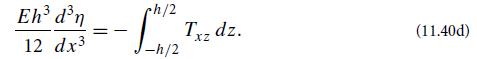


![]()

Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





