We developed the theory of real-valued random processes that vary randomly with time t (i.e., that are
Question:
We developed the theory of real-valued random processes that vary randomly with time t (i.e., that are defined on a 1-dimensional space in which t is a coordinate). Here we generalize a few elements of that theory to a complex-valued random process Φ(x) defined on a (Euclidean) space with n dimensions. We assume the process to be stationary and to have vanishing mean For Φ(x) we define a complex-valued correlation function by
![]()
(where ∗ denotes complex conjugation) and a real-valued spectral density by
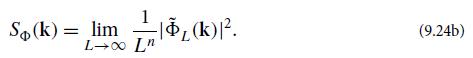
Here ΦL is Φ confined to a box of side L (i.e., set to zero outside that box), and the tilde denotes a Fourier transform defined using the conventions of Chap. 6:
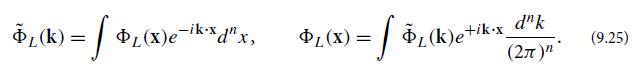
Because Φ is complex rather than real, C(ξ) is complex; and as we shall see below, its complexity implies that [although
![]()
This fact prevents us from folding negative k into positive k and thereby making SΦ(k) into a “single sided” spectral density as we did for real random processes in Chap. 6. In this complex case we must distinguish −k from +k and similarly −ξ from +ξ.
(a) The complex Wiener-Khintchine theorem [analog of Eq. (6.29)] states that
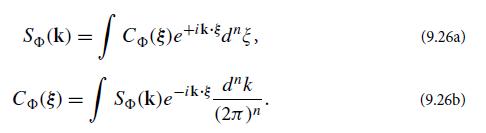
Derive these relations.
Because SΦ(k) is real, this Wiener-Khintchine theorem implies that CΦ(−ξ) = CΦ∗(ξ). Show that this is so directly from the definition (9.24a) of CΦ(ξ). BecauseCΦ(ξ) is complex, the Wiener-Khintchine theorem implies that SΦ(k) ≠ SΦ(−k).
(b) Let ψ(x, t) be the complex-valued wave field defined in Eq. (9.12a), and restrict x to range only over the two transverse dimensions so ψ is defined on a 3-dimensional space. Define
![]()
Show that
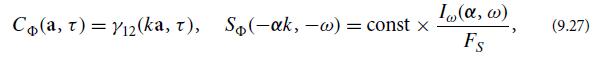
and that the complex Wiener-Khintchine theorem (9.26) is the van Cittert- Zernike theorem (9.22).
Equations

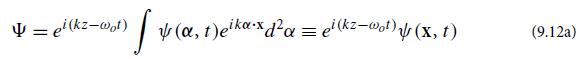
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





