Consider an extension of the Kyle (1985) model with two periods of trading. The fundamental value of an asset is \(v\), which is distributed normally with prior mean \(\mu_{0}\) and variance \(\sigma_{0}^{2}\) known to all agents. Noise traders have demand \(z\), which is distributed normally in each period with mean zero and variance \(\sigma_{z}^{2}\). A single risk-neutral insider observes \(v\) and chooses an asset demand \(x\) in each period as a function of \(v\) to maximize expected two-period profit. For simplicity, profits are not discounted.

With probability \(\pi\), trading occurs in both periods. With probability \(1-\pi\), trading occurs only in the first period, after which fundamental value is revealed.

In trading at period 1, risk-neutral, competitive marketmakers set the price based on their observation of \(x_{1}+z_{1}\) as

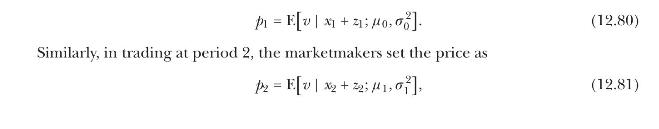
where \(\mu_{1}\) and \(\sigma_{1}^{2}\) are the posterior mean and variance of \(v\) after observation of first-period order flow.
Conjecture a linear equilibrium in which the insider follows the trading rule

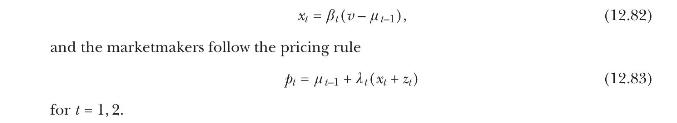
(a) Derive an expression relating the pricing rule parameter \(\lambda_{t}\) to the variances \(\sigma_{t-1}^{2}\) and \(\sigma_{z}^{2}\) and the insider's trading parameter \(\beta_{t}\), for arbitrary (not necessarily optimal) \(\beta_{t}\).

(b) Show that \(\mu_{1}=p_{1}\). Explain.

(c) Derive an expression relating the variance \(\sigma_{1}^{2}\) to the variances \(\sigma_{0}^{2}\) and \(\sigma_{z}^{2}\) and the insider's first-period trading parameter \(\beta_{1}\).

(d) In the second period of trading, the equilibrium is described by the single-period Kyle model, conditional on \(\mu_{1}\) and \(\sigma_{1}^{2}\). Show that the market is deeper in the second period ( \(\lambda_{2}\) is lower) if the insider traded more aggressively in the first period. Explain this fact intuitively.

(e) If in the first period of trading the insider believes that \(\pi=0\), the single-period Kyle model describes trading in that period too. For this case, derive the ratio of market depth in the second period to market depth in the first period, \(\lambda_{1} / \lambda_{2}\). Show that market depth is greater in the second period. Why?

(f) Now consider what happens when the insider understands that \(\pi>0\). Show that the insider trades less aggressively in the first period, and explain why this is so. Discuss intuitively how this affects the relative depth of the market in the two periods.

Transcribed Image Text:

P = E[v] x1 +21; 0, 0] Similarly, in trading at period 2, the marketmakers set the price as 1=E[v] x +22; 1,07], (12.80) (12.81)