Denote by (mathcal{H}^{1}) the Cameron-Martin space (13.2) and by (mathcal{H}_{circ}^{1}) the set defined in (13.3). a) Show
Question:
Denote by \(\mathcal{H}^{1}\) the Cameron-Martin space (13.2) and by \(\mathcal{H}_{\circ}^{1}\) the set defined in (13.3).
a) Show that \(\mathcal{H}^{1}\) is a Hilbert space with the canonical norm \(\|h\|_{\mathcal{H}^{1}}^{2}:=\int_{0}^{1}\left|h^{\prime}(s)\right|^{2} d s\) and scalar product \(\langle\phi, hangle_{\mathcal{H}^{1}}=\int_{0}^{1} \phi^{\prime}(s) d h(s)\) (this is a Paley-WienerZygmund integral, cf. 13.5).
b) Show that \(\mathcal{H}_{\circ}^{1}\) is a dense subset of \(\mathcal{H}^{1}\).
c) Show that \(\|h\|_{\mathcal{H}^{1}}=\sup _{\phi \in \mathcal{H}^{1},\|\phi\|_{\mathcal{H}^{1}=1}}\langle\phi, hangle_{\mathcal{H}^{1}}=\sup _{\phi \in \mathcal{H}_{0}^{1},\|\phi\|_{\mathcal{H}^{1}}=1}\langle\phi, hangle_{\mathcal{H}^{1}}\).
d) Let \(h \in \mathcal{C}_{(0)}[0,1]\). Show that \(h otin \mathcal{H}^{1}\) if, and only if, there exists a sequence \(\left(\phi_{n}\right)_{n \geqslant 1} \subset \mathcal{H}_{\circ}^{1}\) such that \(\left\|\phi_{n}\right\|_{\mathcal{H}^{1}}=1\) and \(\left\langle\phi_{n}, h\rightangle_{\mathcal{H}^{1}} \geqslant 2 n\).
Data From (13.2)
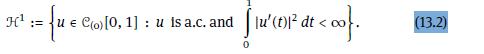
Data From (13.3)
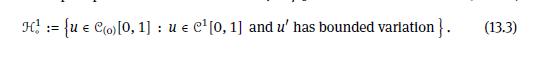
Step by Step Answer:

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook
ISBN: 9783110741254
3rd Edition
Authors: René L. Schilling, Björn Böttcher





